Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Исходные данные для типового расчета

1. Найдем сначала недостающие значения параметров. Известно, что наша случайная величина распределена с постоянной плотностью 0, 35 в интервале (–3; q ₂), попадает с вероятностью 0, 30 в интервал (0, 2) и имеет там плотность распределения
φ (x) = A ·| x – 2|.
Находим вероятность попадания случайной величины Х в интервал (–3; q ₂):
P (–3 < X < q ₂) = 1 – 0, 3 = 0, 7.
C другой стороны, вероятность этого события можно найти как площадь криволинейной трапеции (в нашем случае прямоугольника), расположенной над интервалом (–3; q ₂) и ограниченной сверху кривой распределения, P (–3 < X < q ₂) = 0, 35·(q ₂ – (–3)) = 0, 7. Отсюда получаем q ₂ = –1.
Вероятность попадания случайной величины X в интервал (0; 2) можно вычислить с помощью интеграла (2.3):

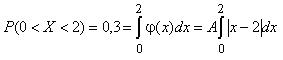
Так как для x є (0, 2) | x – 2| = 2 – x, то

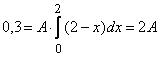
2. Теперь можно записать плотность распределения вероятностей нашей случайной величины X:

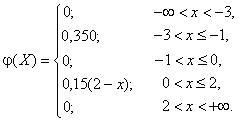
На рис. 3 представлен график функции плотности у = φ (x).

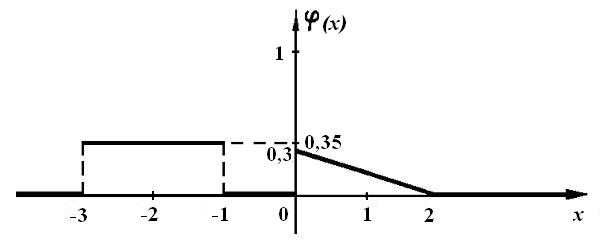
Рис. 3

Далее отметим, что в каждой точке х значение функции F (x) равно площади криволинейной трапеции, ограниченной сверху кривой распределения, снизу осью 0 х и лежащей левее перпендикуляра, восстановленного из точки х, поэтому уже сейчас можем приближенно построить график функции F (x).
В интервалах, где φ (х) = 0, функция F (x), очевидно, постоянна, причем для x ≤ –3, F (x) ≡ 0, при x ≥ 2 F (x) ≡ 1, а в интервале (–1; 0) F (x) = 0, 7 = Р (–3 < X < –1).
Далее, при движении х вправо внутри интервала (–3; –1) F (x) “равномерно” возрастает от 0 до 0, 7 – поэтому здесь ее график представляет собой отрезок прямой, соединяющий точки (–3; 0) и (–1; 0, 7). Внутри интервала (0; 2) функция F (x) растет не равномерно: к концу интервала рост F (x) уменьшается и совсем прекращается в т. x = 2. Ясно, что в этом интервале график функции F (x) представляет собой отрезок параболы, ветви которой направлены вниз, с вершиной в точке (2; 1). Так как F (x) – непрерывная функция, то парабола должна проходить через точку (0; 0, 7). Построенный таким образом график функции распределения y = F (x) изображен на рис. 4.

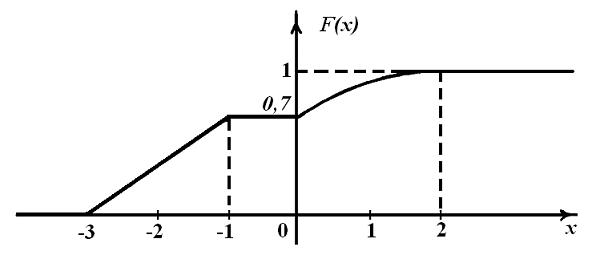
Рис. 4

3. Найдем функцию распределения случайной величины Х аналитически согласно (2.5).
Для х є (–∞; –3]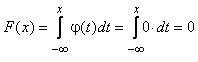
для х є (–3; –1]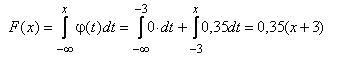
для х є (–1; 0]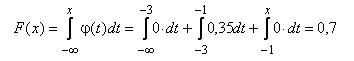
для х є (0; 2]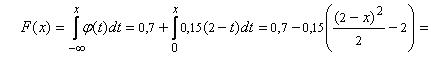
= 1 – 0, 0075(x – 2)²
И далее F (x) = 1(x > 2).
Итак, выпишем функцию распределения

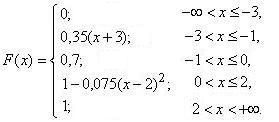
и сопоставим ее с графиком функции F (x), полученным выше: они полностью соответствуют друг другу.
4. Найдем числовые характеристики случайной величины X:
а) математическое ожидание (2.10):

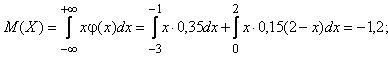
б) дисперсию (2.11):

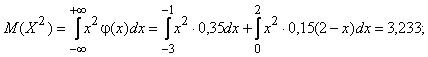
D (X) = M (X ²) – M (X))² = 3, 233 – (–1, 2)² = 1, 793;
в) среднее квадратичное отклонение

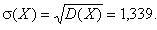
5. Вычислим вероятность события по формуле (2.3)
P (| X – M (X)| < σ (X)) = P (–1, 2 – 1, 339 < X < –1, 2 + 1, 339) =

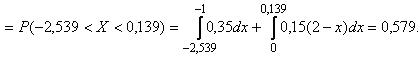
Для контроля вычислим вероятность того же события, используя функцию распределения (2.7).
P (–2, 539 < X < 0, 139) = F (0, 139) – F (–2, 539) = 0, 579.
6. Найдем медиану m_X случайной величины X. По определению
P (X < m_X) = P (X > m_X) = 0, 5,
т.е. площади двух криволинейных трапеций, ограниченных кривой распределения и расположенных слева и справа от m_X, должны быть равны. Поэтому очевидно, что в нашем случае точка m_X должна принадлежать интервалу (–3; –1). Имеем:
– 3 < x ≤ 1; F (x) = 0, 35(x + 3).
Решая уравнение F (x) = 1/2, находим медиану
m_X = – 11/7 = – 1, 571.