Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Теоретическое введение. Непрерывные случайные величины

Непрерывные случайные величины

Теоретическое введение

Случайная величина Х имеет непрерывное распределение, если она может принимать любые значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно. Строгое определение непрерывной случайной величины следующее: случайная величина называется непрерывной, если математическое ожидание любой функции g (X) можно записать в виде:

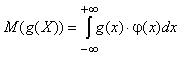
(2.1)

Под “любой” функцией g (х) имеется ввиду такая, для которой интеграл (2.1) существует и сходится абсолютно.
Функция φ (x) называется плотностью распределения вероятностей непрерывной случайной величины Х и обладает следующими свойствами:
1. Вероятность попадания величины X в произвольный интервал на оси 0 x равна

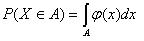
(2.2)

т.е. интегралу по А от функции плотности.
Таким образом, функция плотности φ (x) полностью характеризует распределение случайной величины Х.
2. В частности, для интервала (x ₁, x ₂), получаем:

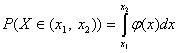
(2.3)

3. Так как вероятность неотрицательна, то из (2.2) следует, что φ (x) ≥ 0 для любого x.
4. Вероятность достоверного события равна 1, поэтому

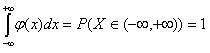
(2.4)

Последнее равенство называется условием нормировки функции плотности.

График функции плотности распределения φ (x) называется кривой распределения (рис. 1).

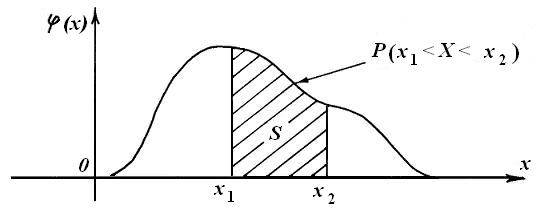
Рис. 1. График плотности распределения φ (x) (кривая распределения)

Вероятность попадания случайной величины Х в интервал (x ₁, x ₂) численно равна площади соответствующей криволинейной трапеции. Из условия нормировки следует, что площадь области, ограниченной сверху кривой распределения, а снизу – осью 0 х, равна 1.
Функцией распределения случайной величины Х является функция F (x), равная вероятности события (Х < x), т.е. вероятности того, что случайная величина Х примет значение, меньшее значения аргумента х.
Для непрерывной случайной величины функция распределения равна

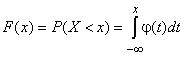
(2.5)

и обладает следующими свойствами:
1. 0 ≤ F (x) ≤ 1 для всех x;
2. F (–∞) = 0, F (+∞) = 1;
3. F (x) – неубывающая функция на всей оси;
4. F (x) – непрерывная функция, в точках непрерывности φ (x) она имеет производную:

Вероятность попадания непрерывной случайной величины Х в произвольный интервал (x ₁, x ₂) можно вычислить с помощью функции распределения следующим образом:

Поэтому функция распределения F (х) так же, как и функция плотности распределения φ (x), полностью характеризует распределение вероятностей случайной величины Х и даже более удобна для расчетов вероятностей, так как не требует интегрирования.
В задачах статистики часто бывает нужно найти такое значение х по заданной вероятности Ρ, что

Данное уравнение может иметь, вообще говоря, множество решений. Но для большинства распределений, встречающихся в статистике, функция плотности распределения φ (x) строго положительна для всех Х из некоторого интервала и равна нулю вне этого интервала. Поэтому внутри этого интервала функция F (x) строго монотонно возрастает.
В этих случаях решение уравнения (2.8) существует и единственно для всех Ρ є (0; 1). Оно называется квантилью распределения и обозначается х _Ρ (рис. 2).

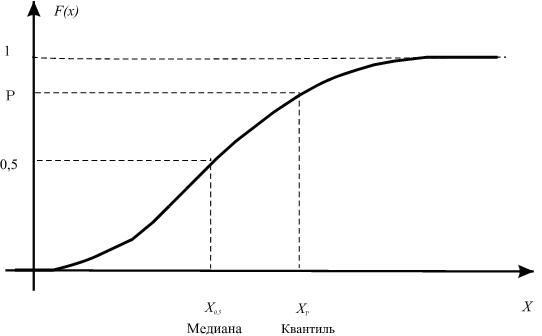
Рис. 2. График функции распределения, квантиль и медиана случайной величины Х

Некоторые квантили имеют специальное название. Так, медианой непрерывной случайной величины Х называется действительное число m_X, удовлетворяющее условию:

т. е. решение уравнения F (x) = 0, 5.
Математическое ожидание и дисперсия непрерывной случайной величины Х находят по формулам, которые следуют из выражения (2.1):

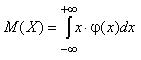
(2.10)

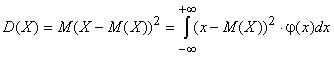
Дисперсию проще рассчитывать по следующей формуле:

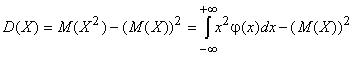
(2.11)

Содержание типового расчета

Непрерывная случайная величина Х распределена с постоянной плотностью С в интервале (q ₁, q ₂), попадает с вероятностью R в интервал (z ₁, z ₂) и имеет там плотность распределения вида φ (x) = A ·| x – z ₃|. Вне указанных интервалов функция плотности равна нулю. Значения некоторых параметров указаны в условии типового расчета.
Требуется:
1. Найти недостающие значения параметров.
2. Найти плотность распределения и функцию распределения случайной величины Х и построить их графики.
3. Вычислить математическое ожидание М (Х), дисперсию D (X) и среднее квадратическое отклонение σ (X) случайной величины Х.
4. Вычислить вероятность события P (| Х – М (Х)| < σ (Х)) двумя способами: с помощью функции плотности распределения и функции распределения.
5. Найти медиану случайной величины Х.