
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сравнение выборок
|
|
Чтобы решить вопрос, принадлежат ли разные выборки одной совокупности, можно воспользоваться статистическими методами проверки гипотез, в частности нуль-гипотезы. Нуль-гипотеза строится на предположении о неразличимости статистических критериев выборок при заданной доверительной вероятности. Подтверждение нуль-гипотезы, полученное из сравнения экспериментальных и табулированных статистических оценок, говорит о принадлежности сравниваемых выборок к одной совокупности. В зависимости от имеющихся исходных сведений для проверки выполнения нуль-гипотезы можно использовать разные критерии и решать разные проблемы.
Если известны дисперсии или стандартные отклонения разных выборок, можно сравнить их и решить вопрос о принадлежности этих выборок одной совокупности по воспроизводимости. Например, можно сравнить воспроизводимость двух методов определения одной и той же величины.
При этом целесообразно использовать статистический критерий F -распределения (F -критерий, или критерий Фишера).

где V1 > V2 или s21 > s22.
Нуль-гипотеза строится на предположении о неразличимости дисперсий или стандартных отклонений. Рассчитывают F-критерий по экспериментальным данным. Сравнивают найденное значение Fэксп с табличным значением Fтабл при заданных доверительных вероятностях и числе степеней свободы в выборках.
Если Fэксп < Fтабл; нуль-гипотеза подтверждается, если Fэксп > Fтабл отвергается.
пример 18. Получены следующие результаты определения марганца в стали (%): 0.80; 0.81; 0.78; 0.83 (фотометрическим методом); 0.76; 0.70; 0.74 (спектральным методом). Сравните воспроизводимость методов (при доверительной вероятности 0.95).
Решение. Вычисляем дисперсии обеих выборок:
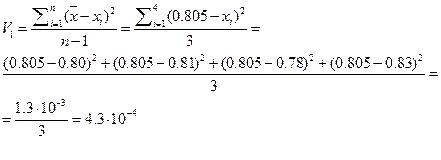
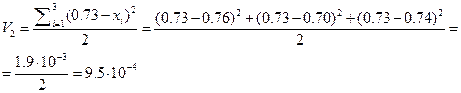
Рассчитываем Fэксп учитывая, что V2 > V1:
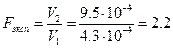
Находим Fтабл (P = 0.95), учитывая, что числа степеней свободы выборки с большей дисперсией стоят в горизонтальном ряду таблиц, а числа степеней свободы выборки с меньшей дисперсией — в вертикальном ряду: Fтабл = 9.6. Как видно, Fэксп< Fтабл) следовательно, воспроизводимость фотометрического и спектрального методов определения марганца одинакова.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Установив однородность дисперсий выборок, можно решать вопросы о принадлежности единичных результатов выборок к одной совокупности и о правильности того или иного метода определения.
Если известны средние выборок с однородной дисперсией, можно судить о принадлежности всех результатов одной выборке. Сравнение средних позволяет решить ряд важных задач, например установить идентичность материалов, выявить систематическую погрешность измерения на разных приборах.
Запишем выражения для истинных значений выборок:
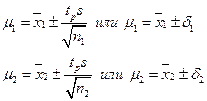
Стандартное отклонение s рассчитывают по данным объединенной выборки.
Нуль-гипотеза строится на предположении об идентичности m1 и m2, т.е. незначимости различия 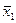 и
и 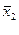 :
:
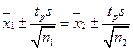
После преобразования получаем:
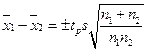
Здесь 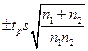 - доверительный интервал
- доверительный интервал 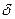 для объединенной выборки.
для объединенной выборки.
Если 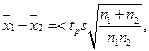 нуль-гипотеза подтверждается.
нуль-гипотеза подтверждается.
Если 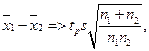 нуль-гипотеза отвергается.
нуль-гипотеза отвергается.
Можно поступить и по-другому: сравнить значения t- коэффициента tэксп рассчитанного по экспериментальным данным, с табличным значением tтабл лри заданной доверительной вероятности:
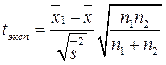
Если tэксп < tтабл нуль-гипотеза подтверждается, если tэксп > tтабл нуль-гипотеза отвергается.
пример 19. Можно ли объединить результаты определений марганца в стали, приведенные в примере 18, для нахождения истинного содержания?
Решение. Для решения вопроса об объединении выборок сравним их среднее, создав нуль-гипотезу с привлечением t -критерия. Поскольку воспроизводимость обоих методов одинакова (пример 18), объединяем выборки для вычисления стандартного отклонения.
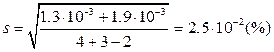
Вычисляем разность ê 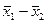 ê по статистическим критериям, находя по таблицам t -коэффициент при Р = 0.95 и ¦ = 5:
ê по статистическим критериям, находя по таблицам t -коэффициент при Р = 0.95 и ¦ = 5:
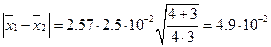
Экспериментально наблюдаемая разность ê 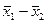 ê = 0.805 — 0.73 = 7.5•10-2 больше расчетной, следовательно, нуль-гипотеза не подтверждается и результаты определения марганца объединять нельзя. По-видимому, в одном из методов допущена систематическая погрешность.
ê = 0.805 — 0.73 = 7.5•10-2 больше расчетной, следовательно, нуль-гипотеза не подтверждается и результаты определения марганца объединять нельзя. По-видимому, в одном из методов допущена систематическая погрешность.
пример 20. Можно ли смешать остатки медного купороса из двух склянок, если при определении в нем воды методом отгонки получены следующие результаты (%):
1 склянка 36.40; 36.54; 36.71
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
2 склянка 35.90; 35.95; 36.08
Доверительная вероятность 0.95.
Решение. Рассчитываем среднее в каждой выборке:
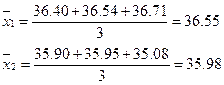
Находим стандартное отклонение, объединяя обе выборки:
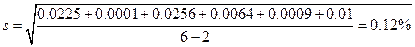
Проверяем нуль-гипотезу:
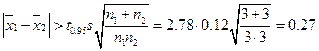
Экспериментальная разность средних ê 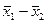 ê = 36.55 — 35.98 = 0.57 больше доверительного интервала d, следовательно, нуль-гипотеза отвергается. Смешивать реактивы из этих склянок не следует.
ê = 36.55 — 35.98 = 0.57 больше доверительного интервала d, следовательно, нуль-гипотеза отвергается. Смешивать реактивы из этих склянок не следует.
Если известно истинное значение какой-либо величины и среднее выборки, сравнение их позволяет установить наличие или отсутствие систематической погрешности.
Например, анализируя стандартный образец, можно оценить правильность результатов, полученных по новой методике. Для этого используют выражение для доверительного интервала:
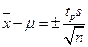 или, если имеется значение s,
или, если имеется значение s,
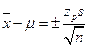
Нуль-гипотеза основывается на предположении о незначимости различия между 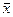 и m.
и m.
По экспериментальным данным вычисляют доверительный интервал при заданной доверительной вероятности и числе степеней свободы и сравнивают с экспериментально найденной разностью 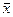 и m.
и m.
Если  гипотеза подтверждается,
гипотеза подтверждается,
Если 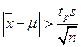 гипотеза отвергается.
гипотеза отвергается.
Как и для средних, можно также сравнивать расчетный и табличный t -коэффициенты.
пример 21. Допущена ли систематическая погрешность при фотометрическом определении хрома по новой методике в стандартном образце стали с содержанием хрома 0.35%, если получены следующие результаты (%): 0.30; 0.34; 0.33;
0.29? Доверительная вероятность 0.95%.
Решение.
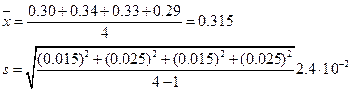
Вычисляем доверительный интервал при Р=0, 95 и f=3:
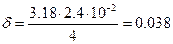
Экспериментально найденная разность, равная ê 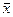 и m½ = |0.315-0.35| =0.035 меньше доверительного интервала, следовательно, нуль-гипотеза подтверждается. Систематическая погрешность отсутствует.
и m½ = |0.315-0.35| =0.035 меньше доверительного интервала, следовательно, нуль-гипотеза подтверждается. Систематическая погрешность отсутствует.
Правила суммирования погрешностей
Способ вычисления суммарной погрешности определяется видом погрешности (абсолютной или относительной, систематической или случайной) и родом арифметических действий над экспериментальными значениями.
Систематические погрешности
Если известны как величины, так и знаки систематических погрешностей, то можно руководствоваться следующими правилами.
Абсолютная погрешность суммы
х = а + b + с
равна сумме абсолютных погрешностей слагаемых:
Dx = Da + Db + Dс
где Dx — суммарная погрешность; а, b и с — значения определяемых величин; Da, Db и Dc — соответствующие абсолютные погрешности.
Абсолютная погрешность разности х = а — b равна разности абсолютных погрешностей:
Dx = Da - Db
Относительная погрешность произведения х = а • b равна сумме относительных погрешностей сомножителей:
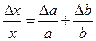
Относительная погрешность частного х = 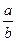 равна разности относительных погрешностей числителя и знаменателя:
равна разности относительных погрешностей числителя и знаменателя:
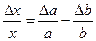
Относительная погрешность степени х = аp равна относительной погрешности величины, возводимой в степень, умноженной на показатель степени:
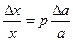
Абсолютная погрешность логарифма х = lg а равна относительной погрешности логарифмируемой величины, умноженной на 0, 434:
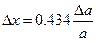
На практике, однако, знаки систематических погрешностей составляющих редко бывают известны. В этом случае применимы приведенные выше формулы, за исключением двух случаев:
погрешность разности |Dx| = |Da| + |Db|
погрешность частного 
Случайные погрешности
Абсолютное стандартное отклонение суммы и разности равно квадратному корню из суммы квадратов абсолютных стандартных отклонений, т.е. для суммы х = а + b и разности х = а — Ь:
Относительное стандартное отклонение произведения и частного равно квадратному корню из суммы квадратов относительных стандартных отклонений сомножителей т. е. для произведения х = а • b и частного х = 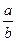 :
:
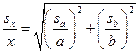
Относительное стандартное отклонение степени равно относительному стандартному отклонению величины, возводимой в степень, умноженной на показатель степени т.е. для х = аР:

Абсолютное стандартное отклонение логарифма равно относительному стандартному отклонению логарифмируемой величины, умноженной на 0.434:
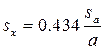
Как видно из приведенных правил, погрешность суммы или разности определяется абсолютными величинами погрешностей, а погрешность произведения или частного — относительными величинами. Однако определив относительную погрешность, можно при необходимости рассчитать абсолютную погрешность и, наоборот, зная абсолютную погрешность найти относительную погрешность.
пример 22. Найдите абсолютную и относительную погрешности при определении общей массы нескольких изделий из платины. Масса каждого изделия была определена с помощью весов с разной систематической погрешностью (г):
платиновый тигель 4.05 (+0.01), платиновые чашки 27.84 (+0.02), крышки тигля 2.18 (—0.03), наконечники к щипцам 3.44 (+0.01).
Решение. Находим абсолютную погрешность определения общей массы: Dm = 0.91 + 0.02 + (-0.03) + 0.01 = +0.01
Для нахождения относительной погрешности сначала находим общую массу изделий:
m = 4.05 + 27.84 + 2.18 + 3.44 = 37.51
Тогда
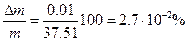
пример 23. Найдите абсолютную и относительную погрешности общей массы трех платиновых тиглей, если при взвешивании тиглей получены следующие массы каждого (г): 6.07; 10.40; 8.33 с соответствующими относительными погрешностями 0.3%; -0.5%; 1.0%.
Решение. Находим абсолютные погрешности массы каждого тигля:
Dm1 = 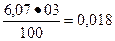
Dm2= 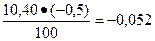
Dm3 = 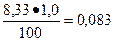
По правилу абсолютных погрешностей суммы:
Dm = 0.018 + (-0.052) + 0.083 = 0.049
Общая масса тиглей равна
m = 6.07 + 10.40 + 8.33 = 24.80
Находим относительную погрешность общей массы:
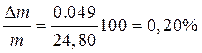
Пример 24. Найдите абсолютную систематическую погрешность для концентрации раствора, приготовленного растворением 100.00 г сульфата меди (погрешность взвешивания 20 мг) в колбе объемом 200.0 мл (погрешность измерения объема —0.2 мл).
Решение. Концентрацию раствора рассчитываем по формуле:
c = 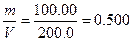 г/мл
г/мл
Далее находим относительную погрешность каждой из величин, входящих в вышеприведенную формулу:
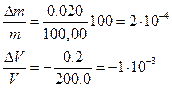
Следовательно, относительная погрешность концентрации равна
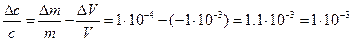
а абсолютная погрешность
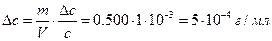
пример 25. Слили по 100 мл растворов соляной кислоты с концентрацией (г/л): 0.50 (±0.02), 3.11 (±0.01) и 1.80 (±0.03). (В скобках указаны стандартные отклонения.) Найдите абсолютное стандартное отклонение для концентрации полученного раствора.
|
|
