
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Виды погрешностей
|
|
По происхождению погрешности химического анализа классифицируют на систематические и случайные.
Систематические погрешности обусловлены постоянно действующими причинами. Такие погрешности можно выявить, устранить или учесть при расчетах. Они постоянны во всех измерениях или изменяются с определенной закономерностью. Систематические погрешности имеют определенный знак.
Случайные погрешности возникают в результате неконтролируемых изменений в условиях измерения. Случайные погрешности нельзя измерить и учесть, но можно оценить по законам математической статистики.
Величина систематической погрешности служит оценкой правильности измерения или метода измерения. Правильность отражает близость полученного результата к истинному. Истинное значение обычно неизвестно. Сравнение часто проводят с действительным значением. Действительное значение a — это экспериментально полученное или расчетное значение, настолько близкое к истинному, что может быть использовано вместо него. За действительное значение, например, может быть принято содержание определяемого компонента в стандартном образце.
Случайные погрешности характеризуют разброс результатов в серии измерений и определяют воспроизводимость измерений или метода.
Погрешности можно выразить абсолютной и относительной величинами.
D = x i - m.
Здесь D — абсолютная погрешность (в тех же единицах, что и измеряемая величина); Xi — единичное измерение; m — истинное значение.
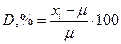
или
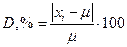
Здесь D — относительная погрешность (в процентах).
пример 1. В стандартном образце сплава с содержанием магния 1.2•10-2% атомно-абсорбпионным методом найдено 1.1•10-2% магния. Рассчитайте абсолютную и относительную погрешности.
Решение. D = 1.1•10-2 - 1.2•10-2 = -1.0•10-3%
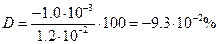
Оценка воспроизводимости
Результат единичного измерения не может служить надежной оценкой содержания определяемого компонента в образце или основой для серьезных выводов из экспериментальных данных. Для получения надежного результата проводят серию параллельных измерений в идентичных условиях. Результат единичного измерения в такой серии называется вариантой, а вся серия — образует ряд вариант, выборочную совокупность или просто выборку.
Центр распределения выборки
В качестве центра распределения используют среднее 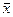 (реже медиану М):
(реже медиану М):
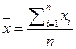
где x i — единичный результат серии (варианта); n — число вариант.
Медиана М — это единичный результат, относительно которого число полученных результатов с большим и меньшим значениями одинаково. При нечетном количестве результатов медиана совпадает с центральным числом выборки, при четном она является средним арифметическим двух центральных результатов.
пример 2. Найдите среднее и медиану результатов определения сульфат-иона в растворе серной кислоты (%): 24.05; 24.21; 24.33; 24.05; 24.22.
Решение. Находим среднее:
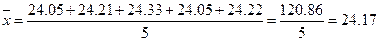
Для нахождения медианы располагаем результаты в порядке возрастания: 24.05; 24.05; 24.21; 24.22; 24.33. В данном случае медианой является центральный результат
М = 24.21
пример 3. Найдите медиану результатов определения влажности почвы (%): 5.31; 4.99; 5.26; 5.10.
Решение. Запишем выборку в порядке возрастания вариант:
4.99; 5.10; 5.26; 5.31. В данном случае имеется два центральных значения, поскольку число результатов четное; поэтому
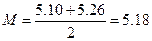
Критерии воспроизводимости
Критериями воспроизводимости служат а) отклонение от среднего,
б) среднее отклонение от среднего,
в) отклонение и среднее отклонение от медианы,
г) размах варьирования,
д) дисперсия и
е) стандартное отклонение.
Отклонения могут быть выражены как абсолютными, так и относительными величинами.
Отклонение от среднего. Отклонение от среднего d — это разность между единичным результатом и средним без учета знака. Среднее отклонение 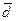 — это среднее арифметическое единичных отклонений:
— это среднее арифметическое единичных отклонений:
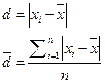
пример 4. Найдите отклонения от среднего и среднее отклонение результатов определения объема колбы (мл): 50.05; 50.15; 49.90; 50.16; 50.00.
Решение. Находим среднее выборки:
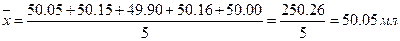
Находим единичные отклонения:
d1 = 50.05 - 50.05 = 0.00
d2 = 50.15 - 50.05 = 0.10
d3 = 49.90 - 50.05 = 0.15
d4 = 50.16 - 50.05 = 0.11
d5 = 50.00 - 50.05 = 0.05
Рассчитываем среднее отклонение:
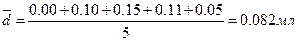
Отклонение от медианы. Отклонение от медианы—это разность между единичным результатом и медианой выборки без учета знака. Среднее отклонение от медианы—это среднее арифметическое отклонений от медианы.
пример 5. Найдите отклонение от медианы и среднее отклонение от медианы результатов, приведенных в примере 4.
Решение. Располагаем выборку в порядке возрастания вариант: 49.90; 50.00; 50.05; 50.15; 50.16. Видим, что М = 50.05 мл.
Находим единичные отклонения:
|49.90 - 50.05| = 0.15
|50.00 - 50.05| = 0.05
|50.05 - 50.05| = 0.00
|50.15 - 50.05| = 0.10
|50.16 - 50.05| = 0.11
Среднее отклонение от медианы равно
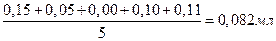
пример 6. Найдите относительное отклонение максимального и минимального результатов в выборке, приведенной в примере 4.
Решение. Находим отклонения:

пример 7. Найдите относительное отклонение второго результата от медианы в выборке примера 4.
Решение, х2 = 50.15 мл
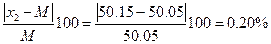
Размах варьирования (диапазон выборки). Размах варьирования w — это разность между максимальным и минимальным значениями выборки
w = xмакс — xмин
пример 8. Каков размах варьирования выборки, приведенной в примере 4?
Решение. Максимальное значение в данной выборке 50.16, минимальное значение 49.90.
w = 50.16 - 49.90 = 0.26 мл
Дисперсия и стандартное отклонение. Более строгими критериями воспроизводимости, чем отклонение и размах варьирования, являются дисперсия и стандартное отклонение.
Следует различать дисперсию и стандартное отклонение генеральной совокупности и выборочной совокупности (т.е. ряда из n вариант или выборки). Генеральная совокупность представляет собой гипотетическую совокупность, охватывающую все мыслимые результаты от 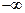 до
до  . Выборочная совокупность — это конечный ряд, включающий n вариант. При n> 20 ряд можно считать с достаточной степенью приближения генеральной совокупностью. В генеральной совокупности среднее и истинное значения совпадают. В выборочной совокупности среднее может отличаться от истинного значения. В генеральной совокупности все результаты и отклонения от среднего—независимые величины, т.е. число степеней свободы ¦ равно числу вариант n. В выборке число степеней свободы равно числу вариант минус число связей, накладываемых на выборку.
. Выборочная совокупность — это конечный ряд, включающий n вариант. При n> 20 ряд можно считать с достаточной степенью приближения генеральной совокупностью. В генеральной совокупности среднее и истинное значения совпадают. В выборочной совокупности среднее может отличаться от истинного значения. В генеральной совокупности все результаты и отклонения от среднего—независимые величины, т.е. число степеней свободы ¦ равно числу вариант n. В выборке число степеней свободы равно числу вариант минус число связей, накладываемых на выборку.
И дисперсия, и стандартное отклонение характеризуют рассеяние вариант относительно среднего. Дисперсию V выборки вычисляют по формуле
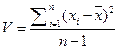
Число степеней свободы меньше числа вариант на единицу, так как исключается степень свободы, связанная с определением среднего. Если известно истинное значение, то
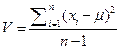
Стандартное отклонение выборки равно квадратному корню из дисперсии, взятому с положительным знаком, и имеет размерность измеряемой величины:
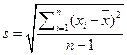
Если известно истинное значение или выборка достаточно велика, используют стандартное отклонение генеральной совокупности s:
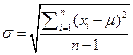
Стандартное отклонение генеральной совокупности и выборки связаны между собой:
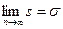
Приближенно стандартное отклонение можно оценить по размаху варьирования:
 или
или 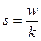
где k — фактор отклонения, приводимый в справочниках для разного числа вариант n.
Используется также относительное стандартное отклонение sr:
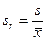
пример 9. Рассчитайте дисперсию и стандартное отклонение (абсолютное и относительное) выборки из примера 4.
Решение. Воспользуемся величинами единичных отклонений, уже рассчитанными в примере 4:
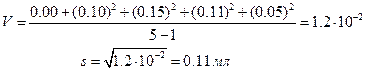
а для вычисления sr возьмем оттуда же значение среднего
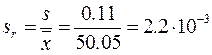
Пример 10. Рассчитайте стандартное отклонение по размаху варьирования выборки из примера 4.
Решение. Возьмем значение w из примера 8. Фактор отклонения k находим в таблицах.
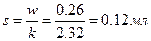
Объединение выборок по воспроизводимости
Оценка воспроизводимости тем надежнее, чем больше число измерений. Число легко выполнимых измерений увеличить нетрудно. При сложных и трудоемких измерениях можно объединить результаты разных выборок, если они получены в идентичных условиях для проб, не очень сильно различающихся по составу. Число степеней свободы объединенной выборки равно суммарному числу вариант объединяемых выборок минус число этих выборок, так как в каждой выборке число степеней свободы на единицу меньше, чем число измерений.
Для объединенной выборки
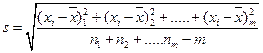
где m — число объединяемых выборок и
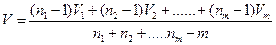
пример 11. Для определения содержания калия в морской воде пламенно-фотометрическим методом отобраны 6 проб. Найдите дисперсию и стандартное отклонение по объединенным результатам:
| № пробы | К, г/л | ||||
| 3.44 | 3.58 | 3.30 | |||
| 2.35 | 2.43 | 2.71 | 2.48 | ||
| 1.11 | 1.05 | ||||
| 1.03 | 0.95 | 1.04 | |||
| 1.80 | 1.95 | 1.83 | |||
| 2.06 | 2.16 | 2.10 | 2.21 | 2.06 |
Решение. Находим среднее, отклонения от среднего, сумму квадратов отклонений и дисперсию для каждой пробы:
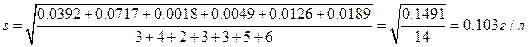
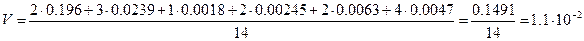
| № пробы | 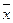
| d | 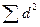
| V |
| 3.44 | 3.44 - 3.44 = 0.00 3.58 - 3.44 = 0.14 3.30 - 3.44 = 0.14 | 0.0000 0.0196 0.0196 Σ = 0.0392 | 0.0196 | |
| 2.49 | 2.35 - 2.49 = 0.14 2.43 - 2.49 = 0.06 2.71 - 2.49 = 0.22 2.48-2.49 = 0.01 | 0.0196 0.0036 0.0484 0.0001 Σ = 0.0717 | 0.0239 | |
| 1.08 | 1.11 - 1.08 = 0.03 1.05 - 1.08 = 0.03 | 0.0009 0.0009 Σ = 0.0018 | 0.0018 | |
| 1.01 | 1.03-1.01 = 0.02 0.95 - 1.01 = 0.06 1.04 - 1.01 = 0.03 | 0.0004 0.0036 0.0009 Σ = 0.0049 | 0.00245 | |
| 1.86 | 1.80 - 1.86 = 0.06 1.95 - 1.86 = 0.09 1.83 - 1.86 = 0.03 | 0.0036 0.0081 0.0009 Σ = 0.0126 | 0.0063 | |
| 2.10 | 2.06 - 2.10 = 0.04 2.16 - 2.10 = 0.06 2.10 - 2.10 = 0.00 2.21 - 2.10 = 0.11 2.06 - 2.10 = 0.04 | 0.0016 0.0036 0.0000 0.0121 0.0016 Σ = 0.0189 | 0.0047 |
Оценка правильности
Если истинное значение известно, то правильность характеризуется разностью между полученным результатом и истинным. Чаще всего истинное значение неизвестно. Тогда оценка правильности производится с использованием данных по воспроизводимости (при условии отсутствия систематической погрешности, что заранее устанавливают специальными приемами). Оценка правильности при этом заключается в нахождении доверительных границ (доверительного интервала 6), в пределах которых с определенной доверительной вероятностью находится истинное значение. Доверительная вероятность Р показывает, сколько вариант из 100 попадает в данный интервал. Иногда вместо доверительной вероятности используют уровень значимости a:
a = 1- Р
Величина Р может выражаться в процентах.
Величина доверительного интервала определяется воспроизводимостью результатов, числом их и доверительной вероятностью. Связь между всеми этими величинами выводится на основе законов нормального распределения для генеральной совокупности и t -распределения для выборочной совокупности.
Для выборки (ряда из n вариант)
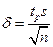
где s — стандартное отклонение выборки; tp — коэффициент Стьюдента, приводимый в таблицах для разных доверительных вероятностей Р и разных степеней свободы:
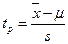
Следовательно,
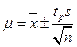
Для генеральной совокупности
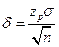
где s — стандартное отклонение генеральной совокупности:
zp — табулированный коэффициент, зависящий от доверительной вероятности Р:
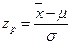
Отсюда
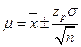
При одной и той же доверительной вероятности коэффициент z меньше, чем коэффициент t, поэтому при использовании z и s получают более узкий доверительный интервал, чем при использовании t и s. При увеличении числа вариант в выборке t ® z. Если предварительно определить s, проделав большое число измерений (³ 20), можно пользоваться коэффициентом z вместо t для оценки доверительного интервала. Такой прием целесообразен при проведении серийных анализов, так как, однажды затратив время и труд на оценку s, можно в дальнейшем ограничиться малым количеством однотипных измерений, сохраняя при этом достаточно узкий доверительный интервал. Помогает в оценке s и объединение выборок.
Располагая статистическими критериями, можно решить вопрос о необходимом и достаточном числе параллельных измерений для получения надежного результата или оценить вероятность попадания результата в определенный интервал при заданном числе измерений.
пример 12. Найдите доверительный интервал и доверительные границы по результатам, приведенным в примере 4 (Р = 0.90).
Решение. Рассчитываем стандартное отклонение, воспользовавшись значениями отклонений от среднего, найденными в примере 4:
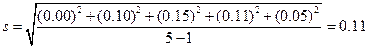
Находим по таблицам коэффициент Стьюдента для ¦ = n—1 = 5—1 = 4
и Р = 0.90 и вычисляем доверительный интервал:
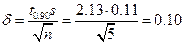
Используя значение среднего (см. пример 4), находим доверительные границы
50.05 + 0.10 = 50.15
50.05 - 0.10 = 49.95
Поскольку недостоверна уже первая цифра после запятой, округляем среднее до 50.0. Итак, доверительные границы результата: 50.1 мл и 49.9 мл.
пример 13. Вернемся к условию примера 11. Найдите доверительные границы и доверительный интервал для среднего первой пробы с доверительной вероятностью 90 и 95%.
Решение. Число результатов в объединенной выборке равно 20, поэтому можно считать ее генеральной совокупностью с достаточным приближением и принять рассчитанное стандартное отклонение s равным s. Находим коэффициент z (при Р = 0.90, Р = 0.95 и ¦ = 2) по таблицам. Следовательно, доверительные интервалы равны:
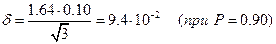
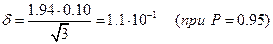
пример 14. При определении калия в морской воде пламенно-фотометрическим методом получены следующие результаты (г/л): 0.94; 0.84; 1.05. Найдите доверительный интервал для среднего с доверительной вероятностью 90%: а) используя только приведенные здесь данные; б) привлекая также данные, приведенные в примере 11.
Решение, а) Вычисляем среднее и стандартное отклонения выборки:
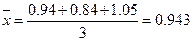
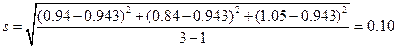
Для выборки из трех вариант следует использовать t- распределение. По таблицам находим коэффициент Стьюдента при Р = 0.90.
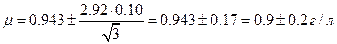
б) Учитывая, что стандартное отклонение объединенной выборки (см. пример 11) можно считать стандартным отклонением генеральной совокупности s, используем коэффициент Z:
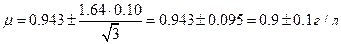
Пример 15. Сколько измерений необходимо при определении рН сыворотки крови с доверительным интервалом 0.01 единицы рН и доверительной вероятностью 95%, если предварительно установлено, что s = 0.0065?
Решение. Поскольку известно s, используем коэффициент z:
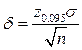
отсюда
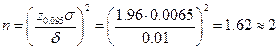
Таким образом, достаточно сделать два измерения.
пример 16. Стандартное отклонение атомно-абсорбционного определения кальция в сыворотке крови, полученное на основании пяти измерений, равно 0.010 мкг/мл. Сколько параллельных определений нужно сделать, чтобы с вероятностью 95% результат определения кальция попал в доверительный интервал 0.020 мкг/мл?
Решение. Запишем выражение для доверительного интервала:
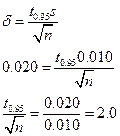
Как видно, в выражение входят две неизвестные величины. Применяем метод подбора: пользуясь таблицами значений t -коэффициентов, подбираем такое n, чтобы соблюдалось условие
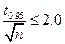
При n=2 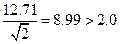
При n=3 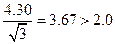
При n=4 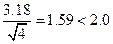
Следовательно, чтобы результат анализа попал в заданный доверительный интервал, необходимо сделать не менее четырех измерений (n ³ 4).
Исключение данных
Для решения вопросов об исключении из серии выпадающего результата существует ряд приемов. Простейший из них, применяемый при п ³ 5, заключается в отбрасывании наибольшего и наименьшего результатов.
Более строгий подход основан на использовании статистических критериев, в частности Q -критерия. В этом случае находят отношение разности между выпадающим и ближайшим к нему результатами к размаху варьирования. Полученное значение Qэксп сравнивают с табличным значением Q-критерия (так называемым критическим значением Qкрит) при заданных доверительных вероятностях и числе результатов.
Если Qэксп > Qкрит, выпадающий результат исключают, и наоборот, если Qэксп < Qкрит; результат исключать нельзя — он принадлежит выборке.
Если выборка очень мала (n = 3), следует провести дополнительные измерения и включить их в выборку. Если такой возможности нет, лучше для дальнейшей обработки пользоваться медианой, а не средним.
пример 17. Получены следующие результаты определения меди в латуни (%): 12.29; 12.24; 12.48; 12.20. Можно ли исключить какой-то результат? (Р = 0.90).
Решение. Выпадающий результат 12.48. Располагаем результаты в порядке возрастания: 12.20; 12.24; 12.29; 12.48.
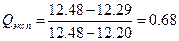
По таблицам: Qкрит = 0.76 при n = 4 и Р = 0.90. Qэксп < Qкрит следовательно, результат 12.48 следует оставить в выборке.
|
|