Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Абсолютна зоряна величина

У середині XIX ст. англійський астроном Норман Погсон удосконалив метод класифікації зір за принципом світності, що існувала з часів Гіппарха і Птолемея. Погсон врахував, що різниць в плані світності між двома класами становить 2, 5 (наприклад, сила світності зорі третього класу в 2, 5 раза більше, ніж у зорі четвертого класу). Погсон увів нову шкалу, за якою відношення між зорями першого і шостого класу становить 100 до 1.

Видимі зоряні величини нічого не говорять ні про загальну енергію, випромінювану зорею, ні про яскравості її поверхні. Дійсно, внаслідок відмінності у відстанях маленька, порівняно холодна зоря тільки через свою відносно значну близькість до нас може мати значно меншу видиму зоряну величину (тобто здаватися яскравіше), ніж далекий гарячий гігант.

Якщо відстані до двох зір відомі, то на підставі їхніх видимих зоряних величин легко знайти ставлення випромінюваних ними дійсних світлових потоків. Для цього достатньо освітленості, створювані цими зірками, віднести до загальної для всіх зір стандартної відстані. За таку відстань приймають 10 пк.

Зоряна величина, яку мала б зоря, якщо її спостерігати з відстані в 10 пк, називається абсолютною зоряною величиною. (При цьому не враховується міжзоряне поглинання світла). Таким чином, абсолютна зоряна величина дозволяє порівнювати питому світність небесних об’єктів у заданому діапазоні спектра.

Як і видимі, абсолютні зоряні величини можуть бути візуальними, фотографічними тощо.

Нехай видима зоряна величина деякої зорі дорівнює т, а відстань її від спостерігача становить г пс. За визначенням, зоряна величина з відстані 10 пк буде дорівнювати абсолютній зоряній величини М. Застосовуючи до т і М формулу, отримаємо:

0, 4(m-M) = lg 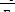(3.1)

де Е і Е₀ — відповідно освітленості від зорі з відстані г пс і 10 пк. Оскільки освітленості обернено пропорційні квадрату відстані, то

= (3.2)

Підставляючи (3.2) в (3.1), отримаємо:

0, 4(m-M) = 21gr-2, (3.3)

або

М = m+5-51gr (3.4)

Формула (3.4) дозволяє знайти абсолютну зоряну величину М, якщо відома видима зоряна величина об’єкта т і відстань до нього г, виражена в парсеках. Якщо ж абсолютна зоряна величина відома з яких-небудь інших міркувань, то, знаючи видиму зоряну величину, легко знайти виражену в парсеках відстань:

lg г = 1 + 0, 2 (т - М) (3.5)

Величина (т—М) називається модулем відстані.

Оскільки річний паралакс % світила і відстань г до нього в парсеках пов язані співвідношенням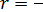

М = т+5+51gn. (3.6)

Як приклад знайдемо абсолютну візуальну зоряну величину Сонця, видима візуальна зоряна величина якого m_Q = -26" *, 72. Підставляючи т₀ і lgr₀ у формулу (3.6), отримуємо абсолютну зоряну величину Сонця:

М₀ = -26 ^m, 72+5^т + 26 ^m, 57 = 4 ^m, 85.