Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Статистическое распределение выборки. Эмпирическая функция распределения
|
|
В теории вероятностей под распределение понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике – соответствие между наблюдаемыми вариантами и их частотами, или относительными частотами.
Пусть из генеральной совокупности объема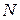 
выбрано 
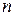объектов. Исследуется признак X со значениями: x1, x2, …xk;
с частотами вариантов: n1, n2, … nk.
Событие X < x1;
X < x2 имеет относительную частоту этого события n1/n;
X < x3 имеет относительную частоту этого события (n1+n2)/n
и т.д.
Таким образом, в общем случае X < x есть функция от x. Эту функцию обозначают: F*(x) и называют эмпирической функцией распределения выборки.
Определение: Эмпирической функцией распределения выборки называется функция F*(x), которая для каждого значения признака x определяет относительную частоту события X < x, т.е.
F*(x) = nx / n,
где nx – число наблюдений, при которых значения вариант оказываются меньше, чем x; n – объем выборки.
Эта функция служит для приближенного представлении о теоретической функции распределения случайной величины.
Основные свойства
1. Значения эмпирической функции принадлежат отрезку [0; 1];
2. F*(x) – неубывающая функция,
т.е. из того, что x2 > x1 следует F*(x2)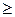 
F*(x1).
3. Если x1 – наименьшая варианта, то F*(x)=0 при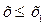 
;
если xk – наибольшая варианта, то F*(x)=1 при x > xk;
(
).
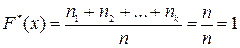Пример. Построить эмпирическую функцию распределения по данной выборке
| хi | ||||
| ni |
Решение. Объем выборки n = 6+16+18+20 = 60. Составим функцию, используя формулу F*(x).
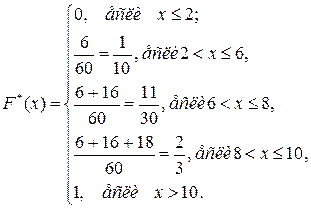
Построим график эмпирической функции распределения.
|
|
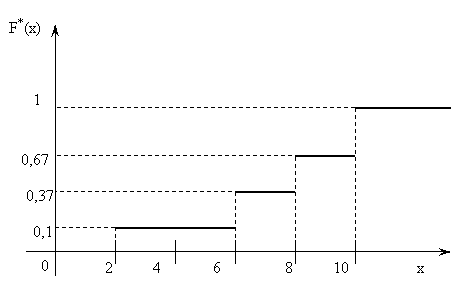