
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Показатели тесноты корреляционной связи
|
|
Задачи корреляционного анализа сводятся к измерению тесноты известной связи между варьирующими признаками, определению факторов, оказывающих наибольшее влияние на результативный признак, а также оценке соответствия уравнения регрессии выявленным причинно-следственным связям.
В качестве показателей тесноты связи между количественными признаками наиболее часто используются линейный коэффициент корреляции и корреляционное отношение (эмпирическое и теоретическое).
Линейный коэффициент корреляции применяется лишь в случае
линейной зависимости между признаками. Он строится на основе отклонений индивидуальных значений х и у отсоответствующей средней величины. В нем учитываются не только знаки, но и значения отклонений 

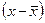 и
и 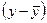 ,, выраженные для сопоставимости в единицах среднего квадратического отклонения каждого признака, т. е. как нормированные отклонения t
,, выраженные для сопоставимости в единицах среднего квадратического отклонения каждого признака, т. е. как нормированные отклонения t
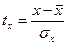 и
и 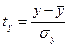 (3)
(3)
Линейный коэффициент корреляции представляет собой среднюю
величину из произведений нормированных отклонений для х и у;
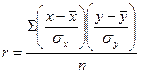 (4)
(4)
где п - число наблюдений.
Формула (4) может быть преобразована:
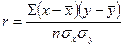 (5)
(5)
Числитель формулы (5), деленный на n, т. е.
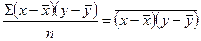 , (6)
, (6)
представляет собой среднее произведение отклонений значений признаков от их средних, именуемое их ковариацией. Поэтому можно сказать, что линейный коэффициент корреляции представляет собой частное от деления ковариации между х и у на произведение их средних квадратических отклонений.
Путем математических преобразований можно получить и другие модификации формулы линейного коэффициента корреляции:
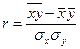 , (7)
, (7)
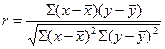 , (8)
, (8)
Для практических вычислений при малом числе наблюдений, n < (20-30), линейный коэффициент корреляции удобнее вычислять по следующей формуле:
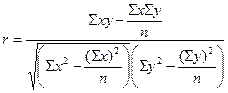 , (9)
, (9)
Линейный коэффициент корреляции можно рассчитать и по формуле:
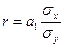 (10)
(10)
где  - коэффициент регрессии в уравнении связи,
- коэффициент регрессии в уравнении связи, 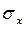 и
и 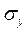 - соответственно среднее квадратическое отклонение в ряду x и в ряду y.
- соответственно среднее квадратическое отклонение в ряду x и в ряду y.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Коэффициент корреляции был предложен английским математиком К. Пирсоном
Значение линейного коэффициента корреляции важно для исследования социально-экономических явлений и процессов, распределение которых близко к нормальному. Он принимает значения в интервале: 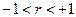 .
.
Отрицательные значения указывают на обратную связь, положительные - на прямую. При r = 0 линейная связь отсутствует. Чем ближе коэффициент корреляции по абсолютной величине к единице, тем теснее связь между признаками. И, наконец, при г = ± 1 связь -функциональная.
Квадрат линейного коэффициента корреляции  называется линейным коэффициентом детерминации. Из определения коэффициента детерминации очевидно, что его числовое значение всегда заключено в пределах от 0 до 1, т. е.
называется линейным коэффициентом детерминации. Из определения коэффициента детерминации очевидно, что его числовое значение всегда заключено в пределах от 0 до 1, т. е. 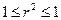 .
.
Теснота корреляционной связи, как и любой другой, может быть измерена эмпирическим корреляционным отношением (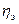 ), когда
), когда 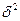 (межгрупповая дисперсия) характеризует отклонения групповых средних результативного признака от общей средней:
(межгрупповая дисперсия) характеризует отклонения групповых средних результативного признака от общей средней:
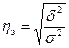 , (11)
, (11)
Подкоренное выражение в формуле (11) представляет собой эмпирический коэффициент детерминации ( 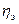 ) который выражается в процентах и показывает, на сколько процентов вариация результативного признака обусловлена вариацией факторного признака. Оба показателя (
) который выражается в процентах и показывает, на сколько процентов вариация результативного признака обусловлена вариацией факторного признака. Оба показателя (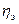 и
и 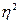 ) были рассмотрены в теме 2.
) были рассмотрены в теме 2.
От эмпирического корреляционного отношения следует отличать -теоретическое.
Теоретическое корреляционное отношение 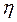 представляет собой относительную величину, получающуюся в результате сравнения среднего квадратического отклонения выровненных значении результативного признака
представляет собой относительную величину, получающуюся в результате сравнения среднего квадратического отклонения выровненных значении результативного признака 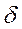 , т. е. рассчитанных по уравнению регрессии, со средним квадратическим отклонением эмпирических (фактических) значений результативного признака
, т. е. рассчитанных по уравнению регрессии, со средним квадратическим отклонением эмпирических (фактических) значений результативного признака 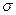 :
:
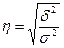 , (11)
, (11)
где 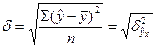 ;
;
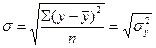
Тогда
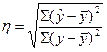 (12)
(12)
Изменение значения 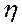 объясняется влиянием факторного признака.
объясняется влиянием факторного признака.
В основе расчета корреляционного отношения лежит правило сложения дисперсий, т.е.  , где
, где 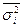 - отражает вариацию у за счет всех остальных факторов, кроме х, т. е. является остаточной дисперсией:
- отражает вариацию у за счет всех остальных факторов, кроме х, т. е. является остаточной дисперсией:
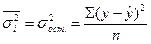
Тогда формула теоретического корреляционного отношения примет вид:
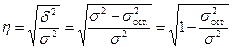 , (13)
, (13)
или 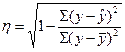 , (14)
, (14)
Подкоренное выражение корреляционного отношения представляет собой коэффициент детерминации (меры определенности, причинности).
Коэффициент детерминации показывает долю вариации результативного признака под влиянием вариации признака-фактора.
Теоретическое корреляционное отношение применяется для измерения тесноты связи при линейной и криволинейной зависимостях между результативным и факторным признаком. При криволинейных связях теоретическое корреляционное отношение, исчисляемое по формулам (13), (14) часто называют индексом корреляции R. При значительной корреляции расчет по формулам (8.9) и (8.10) значительно проще, так как отклонение 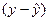 как правило, по значению меньше, чем отклонение
как правило, по значению меньше, чем отклонение 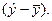
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Значения 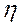 и r совпадают только при наличии прямолинейной связи Несовпадение этих значений свидетельствует, что связь между изучаемыми признаками не прямолинейная, а криволинейная. Уставлено, что если разность квадратов
и r совпадают только при наличии прямолинейной связи Несовпадение этих значений свидетельствует, что связь между изучаемыми признаками не прямолинейная, а криволинейная. Уставлено, что если разность квадратов 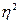 и r 2 не превышает 0.1, то гипотезу о прямолинейной форме связи можно считать подтвержденной.
и r 2 не превышает 0.1, то гипотезу о прямолинейной форме связи можно считать подтвержденной.
Показатели тесноты связи, исчисленные по данным сравнительно небольшой статистической совокупности, могут искажаться действием случайных причин. Это вызывает необходимость проверки их существенности, дающей возможность распространять выводы по результатам выборки на генеральную совокупность.
Для оценки значимости коэффициента корреляции r используют
t -критерий Стьюдента, который применяется при t -распределении, отличном от нормального.
При линейной однофакторной связи t -критерий можно рассчитать по
формуле:
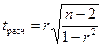 (15)
(15)
где (п - 2) - число степеней свободы при заданном уровне значимости  и объеме выборки п.
и объеме выборки п.
Полученное значение tрасч. сравнивают с табличным значением t -критерия (для 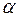 = 0, 05 и
= 0, 05 и 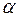 = 0, 01). Бели рассчитанное значение tрасч. превосходит табличное значение критерия tтаблич., то практически невероятно, что найденное значение обусловлено только случайными колебаниями (т. е. отклоняется гипотеза о его случайности).
= 0, 01). Бели рассчитанное значение tрасч. превосходит табличное значение критерия tтаблич., то практически невероятно, что найденное значение обусловлено только случайными колебаниями (т. е. отклоняется гипотеза о его случайности).
Для измерения тесноты зависимости широко используются ранговые коэффициенты корреляции, когда коррелируются не сами значения показателей x и y, а их ранги, т.е. номера их мест, занимаемых в каждом ряду значений по возрастанию или убыванию (обозначаются ранги буквами (R или N).
Коэффициент корреляции рангов Спирмена (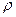 - «ро») рассчитывается по формуле
- «ро») рассчитывается по формуле 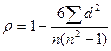 , (16)
, (16)
где  , т.е. разность рангов каждой пары значений x и y, а n – число наблюдений.
, т.е. разность рангов каждой пары значений x и y, а n – число наблюдений.
Коэффициент корреляции рангов Кендела (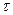 - «тау») определяется по формуле
- «тау») определяется по формуле 
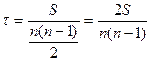 (17)
(17)
Порядок расчета 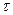 следующий.
следующий.
1. Значения x и y ранжируются, т.е. определяются 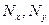 .
.
2. Значения 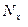 записываются строго в порядке возрастания или убывания.
записываются строго в порядке возрастания или убывания.
3. Ранги второго показателя 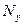 располагаются в порядке, соответствующем значению х в исходных данных.
располагаются в порядке, соответствующем значению х в исходных данных.
4. Последовательно рассматривается каждая пара рангов 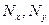 и подсчитывается число следующих за ними пар рангов, у которых
и подсчитывается число следующих за ними пар рангов, у которых 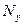 :
:
- более высокого порядка;
- меньше по значению.
Сумма случаев «а» («правильного» следования x и y) учитывается как баллы со знаком «+» и обозначается символом Р.
Сумма случаев «б» (инверсий) учитывается как баллы со знаком «-» и обозначается символом Q.
5. Определяется общая сумма балов, которая обозначается символом S S=P+Q.
6. Полученная сумма сопоставляется с максимальной, которая равна
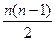 в случае если в обоих рядах ранги следуют строго последовательно от 1 до n.
в случае если в обоих рядах ранги следуют строго последовательно от 1 до n.
Наиболее простым показателем, используемым для измерения тесноты зависимости при параллельном рассмотрении у n единиц значений x и y, является коэффициент Фехнера (коэффициент корреляции знаков).
Он основан на сравнении поведения отклонений индивидуальных значений каждого признака (x и y) от своей средней величины. При этом во внимание принимаются не величины отклонений 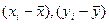 , а их знаки «+» или «-». Определив знаки отклонения от средней величины в каждом ряду, рассматривают все пары знаков и подсчитывают число их совпадений
, а их знаки «+» или «-». Определив знаки отклонения от средней величины в каждом ряду, рассматривают все пары знаков и подсчитывают число их совпадений 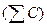 и несовпадений
и несовпадений 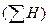 .
.
Коэффициент Фехнера (К ф) рассчитывается как отношение разности чисел пар совпадений и несовпадений знаков к их сумме, т.е. к общему числу наблюдаемых единиц.
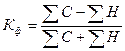 (18)
(18)
Если знаки всех отклонений по каждому признаку совпадают, то 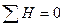 и тогда Кф=1. Это характеризует наличие прямой связи. Если все знаки не совпадают, то
и тогда Кф=1. Это характеризует наличие прямой связи. Если все знаки не совпадают, то 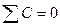 , а Кф=-1, что характеризует обратную связь. Но равенство коэффициента Фехнера единице нельзя оценивать как свидетельство функциональной зависимости между x и y. Поскольку Кф зависит только от знаков и не учитывает величину самих отклонений x и y от их средних величин, но он практически характеризует не столько тесноту связи, сколько ее наличие и направление.
, а Кф=-1, что характеризует обратную связь. Но равенство коэффициента Фехнера единице нельзя оценивать как свидетельство функциональной зависимости между x и y. Поскольку Кф зависит только от знаков и не учитывает величину самих отклонений x и y от их средних величин, но он практически характеризует не столько тесноту связи, сколько ее наличие и направление.
Корреляция рангов может определяться не только для двух, но и для большего числа факторов. Исчисляемый в этом случае показатель именуется коэффициентом конкордации (W). Его формула 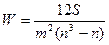 (19), где m – количество коррелируемых факторов;
(19), где m – количество коррелируемых факторов;
n- число наблюдений; S – сумма квадратов отклонений суммы рангов по всем факторам от их средней арифметической, т.е.
|
|
