Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Задания для лабораторных работ
|
|
Задача 1. Написать программу с использованием функторов для определения идеального друга.
Задача 2. Описать родственные связи вашей семьи. В основу построения программы взять предикат родители (мама, папа, ребенок). По ширине правила должны охватывать связи двоюродные братья (сестры), по глубине – дедушка (бабушка) – внуки.
Задача 3. Рекурсивные вычисления в Прологе
1. Вычислить значение гамма-функции
при 
. 
.
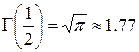2. Вычислить значение интеграла Френеля
с заданной точностью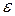 
при заданном значении х (например, 
, 
).
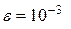3. Вычислить сумму ряда из предыдущей задачи с удержанием заданного количества п членов ряда (например, 4-х членов ряда).
4. Вычислить сумму п первых членов ряда при заданном значении х (например, 
, 
),
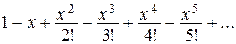
5. Вычислить сумму ряда из предыдущей задачи с заданной точностью (например,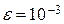 
).
6. Вычислить значение полинома Ермита
.
Граничные условия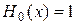 
, 
при 
, 
.
7. Вычислить сумму п первых членов ряда при заданном значении х (например,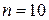 
, 
),
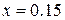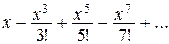
8. Вычислить сумму ряда из предыдущей задачи с заданной точностью (например, ).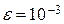
9. Вычислить значение полинома Лагерра
.
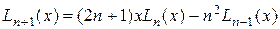Граничные условия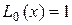 
, 
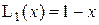при , .
10. Вычислить сумму п первых членов ряда при заданном значении х (например, , ),
11. Вычислить сумму ряда из предыдущей задачи с заданной точностью (например, ).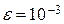
12. Вычислить значение n -го члена ряда Фибоначчи: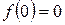 
, 
, 
.
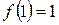13. Вычислить сумму п первых членов ряда при заданном значении х (например, ,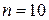 
),
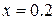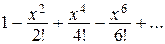
14. Вычислить сумму ряда из предыдущей задачи с заданной точностью (например, ).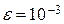
Задача 4. Рекурсивная обработка списков в ПРОЛОГе.
1. Построить список, состоящий из первых 
элементов исходного списка.
2. С двух списков образовать третий, элементами которого были бы положительные элементы первого списка и отрицательные второго.
3. Проверить, следует ли в данном списке элемент у за элементом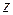 
[x, b, f, c, z, b, e].
4. Определить, между какими двумя элементами заданного списка находится элемент 
[z, k, f, a, ww, ii, w, p].
5. Для данного списка заменить все вхождения элемента 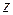на элемент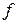 
[k, z, f, z, u, w, z]
6. Исключить из данного списка такой элемент, чтобы сумма элементов, которые остались, была равна 10
[3, 5, 2, 7]
7. Исключить из данного списка элемент, который находится между элементам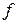и и 
.
[5, a, t, f, s, b, z, b]
8. Из данного списка исключить максимальный элемент.
9. Определить номер элемента k в списке
[s, g, h, e, k, v, d, I, o, p]
10. Разбить данный список на две части: до элемента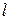 
включительно и остаток
[w, d, s, l, f, e, r, u, h]
11. Прибавить в хвост списка такой элемент, чтобы сумма нового списка была равна S.
12. Построить список, состоящий из положительных элементов исходного списка.
13. Определить элемент списка по его номеру.
14. Построить список, состоящий из последних элементов исходного списка.
15. Исключить из списка второй и четвертый по номеру элементы.
16. Из двух списков образовать третий, элементами которого были бы четные элементы первого списка и нечетные второго.
17. Перестроить данный список в порядке уменьшения элементов.
[15, -1, 21, -3, 1, 2, 3, 4]
18. Из двух списков создать третий, который содержит общие элементы входных списков.
19. Разбить заданный список на три списка равной длины, которые содержат соответственно первую, вторую и третью части входного списка.
20. В данном списке заменить на нуль те элементы, которые меньше среднего арифметического его членов, и на единицу – те, которые больше среднего арифметического.
21. Перестроить список таким образом, чтобы сначала шли все отрицательные, потом нуль и положительные.
Задача 5. Рекурсивные вычисления в ЛИСПе
1. Вычислить значение гамма-функции
при . .
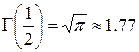2. Вычислить значение интеграла Френеля
с заданной точностью 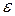при заданном значении х (например, , ).
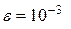3. Вычислить сумму ряда из предыдущей задачи с удержанием заданного количества п членов ряда (например, 4-х членов ряда).
4. Вычислить сумму п первых членов ряда при заданном значении х (например, , ),
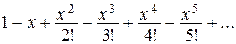
5. Вычислить сумму ряда из предыдущей задачи с заданной точностью (например, ).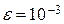
6. Вычислить значение полинома Ермита
.
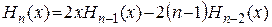Граничные условия 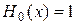, при , .
7. Вычислить сумму п первых членов ряда при заданном значении х (например, , ),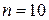
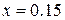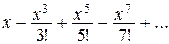
8. Вычислить сумму ряда из предыдущей задачи с заданной точностью (например, ).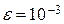
9. Вычислить значение полинома Лагерра
.
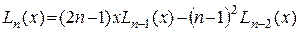Граничные условия 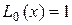, 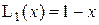при , .
10. Вычислить сумму п первых членов ряда при заданном значении х (например, , ),
11. Вычислить сумму ряда из предыдущей задачи с заданной точностью (например, ).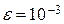
12. Вычислить значение n -го члена ряда Фибоначчи: , , .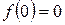
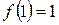13. Вычислить сумму п первых членов ряда при заданном значении х (например, , ),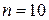
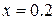14. Вычислить сумму ряда из предыдущей задачи с заданной точностью (например, ).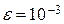
Задача 6. Рекурсивная обработка списков в ЛИСПе.
1. Построить список, состоящий из первых элементов исходного списка.
2. С двух списков образовать третий, элементами которого были бы положительные элементы первого списка и отрицательные второго.
3. Проверить, следует ли в данном списке элемент у за элементом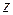
[x, b, f, c, z, b, e].
4. Определить, между какими двумя элементами заданного списка находится элемент
[z, k, f, a, ww, ii, w, p].
5. Для данного списка заменить все вхождения элемента 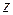на элемент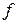
[k, z, f, z, u, w, z]
6. Исключить из данного списка такой элемент, чтобы сумма элементов, которые остались, была равна 10
[3, 5, 2, 7]
7. Исключить из данного списка элемент, который находится между элементам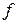и и .
[5, a, t, f, s, b, z, b]
8. Из данного списка исключить максимальный элемент.
9. Определить номер элемента k в списке
[s, g, h, e, k, v, d, I, o, p]
10. Разбить данный список на две части: до элемента 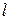включительно и остаток
[w, d, s, l, f, e, r, u, h]
11. Прибавить в хвост списка такой элемент, чтобы сумма нового списка была равна S.
12. Построить список, состоящий из положительных элементов исходного списка.
13. Определить элемент списка по его номеру.
14. Построить список, состоящий из последних элементов исходного списка.
15. Исключить из списка второй и четвертый по номеру элементы.
16. Из двух списков образовать третий, элементами которого были бы четные элементы первого списка и нечетные второго.
17. Перестроить данный список в порядке уменьшения элементов.
[15, -1, 21, -3, 1, 2, 3, 4]
18. Из двух списков создать третий, который содержит общие элементы входных списков.
19. Разбить заданный список на три списка равной длины, которые содержат соответственно первую, вторую и третью части входного списка.
20. В данном списке заменить на нуль те элементы, которые меньше среднего арифметического его членов, и на единицу – те, которые больше среднего арифметического.
21. Перестроить список таким образом, чтобы сначала шли все отрицательные, потом нуль и положительные.
Задача 7. Рекурсивная обработка списков с подсписками в ЛИСПе.
1. Написати функцію, яка знаходить останній атом списку з підсписками.
2. Написати функцію, яка за списком з підсписками знаходить кількість підсписків.
3. Написати функцію, яка за лінійним списком 
будує складний список 
.
4. Написати функцію, яка за лінійним списком будує складний список 
.
5. Написати функцію, яка за лінійним списком будує складний список 
.
6. Знайти кількість атомів списку з підсписками.
7. Знайти глибину списку з підсписками.
8. Знайти найбільший елемент списку з підсписками.
9. Знайти найменший елемент списку з підсписками.
10. Знайти суму елементів матриці.
11. Знайти кількість додатних елементів списку з підсписками.
12. Знайти кількість від’ємних елементів списку з підсписками.
13. Знайти суму елементів списку з підсписками.
14.
|
|