💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Рекурсивные определения и вычисления

Функция называется рекурсивной, если в ее определении содержится вызов самой этой функции. Существует рекурсия по значению, когда вызов является выражением, которое определяет результат функции. Если в результате функции возвращается значение некоторой другой функции и рекурсивный вызов принимает участие в вычислении аргумента этой функции, то имеем рекурсию по аргументу.

Рассмотрим задачу изъятия всех вхождений элемента 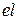из списка 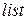. В основе построения функции (DEL_EL el list) положены следующие соображения:

1) из пустого списка невозможно изъять ни одного элемента и потому список-результат является пустым;

2) если известен результат для хвоста, т.е. (DEL_EL el (CDR list)), в случае если текущий элемент (CAR list) будет равен элементу el, то он к результату не присоединяется; в противном случае элемент функцией CAR прибавляется к результату.

Следует отметить, что граничное условие является не только проверкой, является ли входной список пустым. Оно представляет собой последний шаг прямого хода рекурсии, после которого осуществляется присоединение элементов, обозначенных в третьей строке, к вычисленному результату. Это условие обязательно будет выполнено, так как текущие вызовы делаются со списками, которые имеют на элемент меньше чем предыдущие.

(DEFUN DEL_EL (el list)

((NULL list) ())

((EQL el (CAR list)) (DEL_EL el (CDR list)))

(CONS (CAR list) (DEL_EL el (CDR list)))

)

Рассмотрим еще несколько примеров построения функций для рекурсивной обработки списков.

Количество элементов в списке

(defun len (list)

((eql list NIL) 0)

(+ (len (cdr list)) 1)

)

(len '(5 6 2 8 1 9))

Сумма элементов в списке

(defun sum (list)

((eql list NIL) 0)

(+ (sum (cdr list)) (car list))

)

(sum '(5 6 2 8 1 9))

Список, состоящий из первых n элементов исходного списка. В этом случае граничное условие означает, что список, который содержит 0 элементов, является пустым. Первый аргумент будет играть роль счетчика отобранных элементов и его величина уменьшается на единицу при каждом рекурсивном вызове.

(DEFUN DIV (n list)

((zerop n) ())

(cons (car L) (DIV (- n 1) (cdr list)))

)

Список, состоящий из последних n элементов исходного списка. Эта задача является обратной к рассмотренной задаче о функции, которая возвращает входной список из n первых элементов. Отличие в потому, что при каждом рекурсивном вызове голова списка просто уничтожается, а когда счетчик отсчитает заданное количество таких элементов, то, согласно граничному условию, результат становится равным хвосту текущего списка.

(defun N_LAST (n L)

((zerop n) L)

(N_LAST (- n 1) (cdr L))

)

Две последние функции можно объединить в одну, которая из входного списка формирует два, один содержит первые n элементов, а второй – остаток. Отличительной особенностью этой задачи есть то, что надо через одно имя функции возвратить два результата. Вполне естественно у таких случаях сформировать список результатов и соответственно заносить в первый подсписок список последовательно головы списка пока не выполнится граничное условие. В приведенном изображении этой функции использованы локальные определения для переменных w и y, что дает возможность намного упростить понимание работы функции.

(defun N_EL (n l)

((zerop n) nil)

(setq y (cdr l))

(setq w (N_EL (- n 1) y))

(list (cons (car l) (car w)) y)

)

Если имеем список с подсписками и его надо превратить в линейный, то граничное условие означает, что пустой список уже является линеаризованным. Ключевым моментом построения является условие, что когда голова аргумента является подсписком, следующая обработка состоит в ее линеаризации путем рекурсивного вызова и дальнейшем присоединении результата к уже обработанному хвосту аргумента с помощью функции APPEND.

(defun Line (list)

((NULL list) ())

((LISTP (CAT list)) (APPEND (LINE (CAR list) (LINE (CDR list)))

(CONS (CAR list) (LINE (CDR list)))

ПРИМЕРЫ:

1) вычисление факториала:

(defun fact (n)

((zerop n) 1)

(* n (fact (- n 1)))

)

(fact 4)

2) возведение в целочисленную степень:

(defun power (x n)

((zerop n) 1)

(* x (power x (- n 1)))

)

(power 3 4)

3) вычисление суммы ряда cos(x):

(defun cosx (x w n m)

((eql m n) w)

(setq w1 (/ (/ (* (* (- 0 w) x) x) (+ (* 2 m) 1)) (+ (* 2 m) 2)))

(+ w (cosx x w1 n (+ m 1)))

)

(cosx 0.2 1 3 0)