
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Математическое решение задачи
|
|
Первый этап решения – составление матриц однородных преобразований для начальной, конечной и промежуточных точек.
Матрица однородного преобразования, описывающая положение и ориентацию схвата в базовой системе координат Qi(t), имеет вид:
| (2.1) |
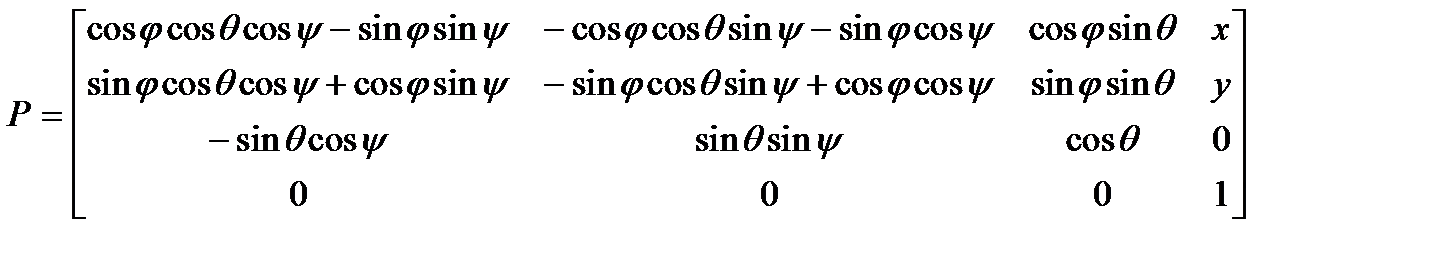 .
.
Подставляя значения углов Эйлера и координат схвата в формулу (2.1), получаем матрицы однородных преобразований для начальной, конечной и промежуточных точек траектории:
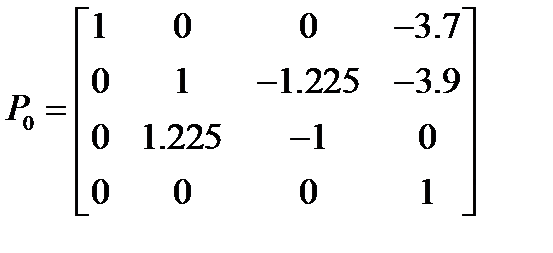 ,
,
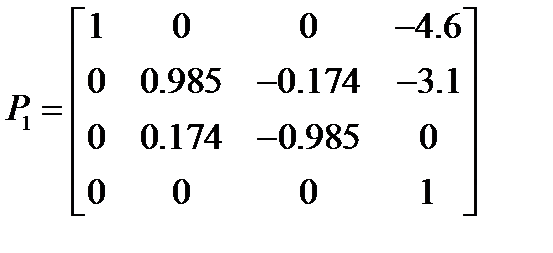 ,
,
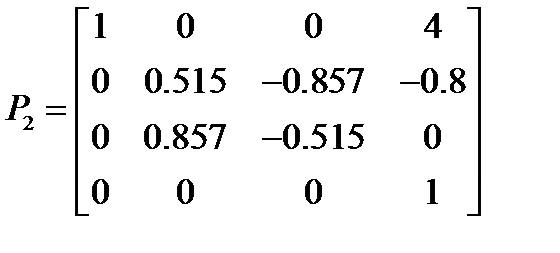 ,
,
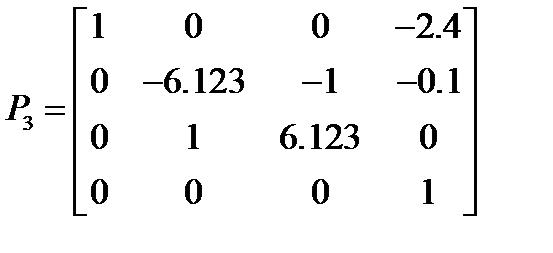 .
.
Второй этап – решение обратной задачи кинематики для каждого звена в начальной, конечной и промежуточных точках. Решим ее с точки зрения алгебраического подхода.
Добавляем к манипулятору еще одну степень подвижности (поворот схвата на угол Q3). Кинематические параметры полученного трехзвенного манипулятора приведены в таблице.2.1.
Таблица.2.1. Кинематические параметры манипулятора
| I | a | a | d | Q |

| Q1 | |||
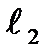
| Q2 | |||
| Q3 |
Матрица, описывающая положение третьего звена (схвата) относительно базовой системы координат, выглядит следующим образом:
| (2.2) |
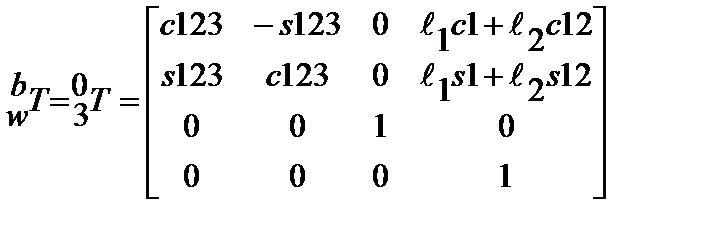 ,
,
где с123=cos(Q1+ Q2+ Q3);
s123=sin(Q1+ Q2+ Q3);
c1=cos(Q1);
c12=cos(Q1+ Q2);
s1=sin(Q1);
s12=sin(Q1+ Q2).
Для рассматриваемого манипулятора матрицу 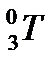 можно записать в виде:
можно записать в виде:
| (2.3) |
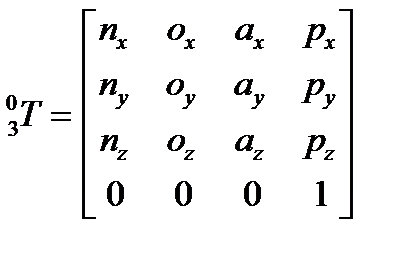 =
= 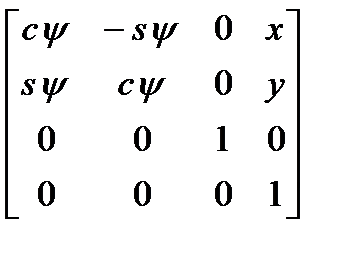 ,
,
где сy=cosy;
sy=siny;
Приравняем выражения (2.2) и (2.3) и получим четыре нелинейных уравнения, которые необходимо решить относительно Q1, Q2, Q3.
| (2.4) |
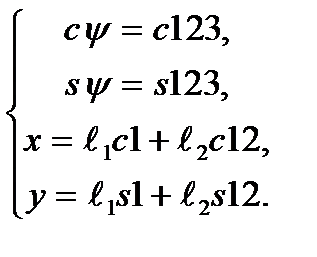
| (2.5) |
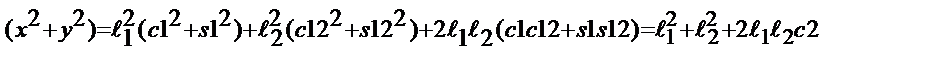 .
.
где с 2 =cosQ2.
Решая уравнение (2.5) относительно с 2, получим
| (2.6) |
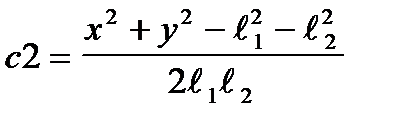 .
.
Для существования решения правая часть уравнения (2.6) должна лежать в пределах [-1…+1]. Если условие выполнено, то находим
| (2.7) |
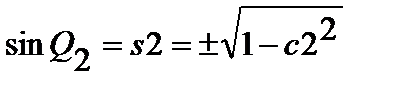 .
.
Выбор знака у sinQ2 соответствует одному из возможных решений. Принимаем положение манипулятора “локоть вниз”, для которого sinQ2 в данном случае принимает положительные значения. При определении угла Q2 воспользуемся функцией ATAN2, которая обеспечивает выбор всех решений и выбор квадранта.
| (2.8) |
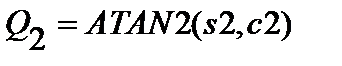 .
.
Зная Q2, воспользуемся двумя последними уравнениями системы (2.4) для определения угла Q1. Перепишем их в следующем виде:
| (2.9) |
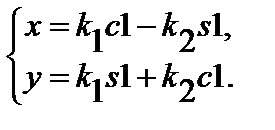
где 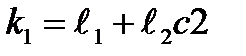 ;
;
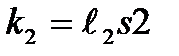 .
.
Для решения уравнений системы (2.9) выполним замену переменных:
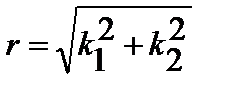 ;
; 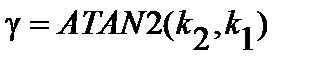 ,
,
тогда
 ;
; 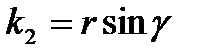 .
.
Теперь систему уравнений (2.9) можно записать следующим образом:
| (2.10) |
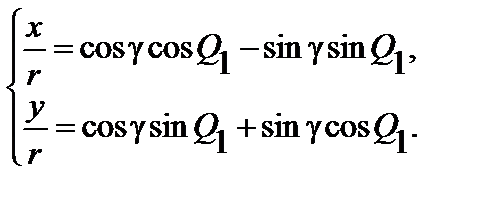
Откуда находим
| (2.11) |
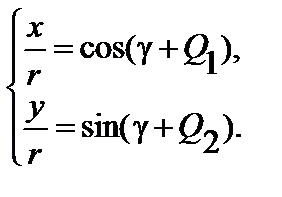
Используя функцию ATAN2, имеем
| (2.12) |

Из первых двух уравнений системы (2.4) находим
| (2.13) |
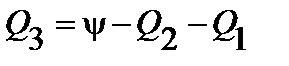 .
.
Подставляя исходные данные в выражения (2.6) – (2.13) и проведя соответствующий расчет, находим значения обобщенных координат для начальной, конечной и промежуточных точек:
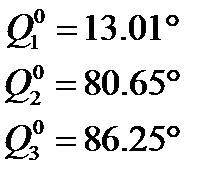 ;
; 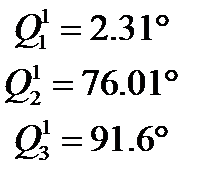 ;
; 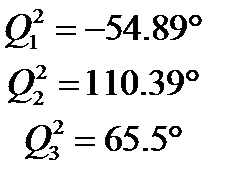 ;
; 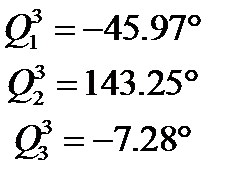 .
.
Третий этап решения – планирование траектории движения манипулятора в обобщенных координатах с учетом интерполяции полиномом Лагранжа, сущность которой заключается в том, что теоретически можно провести непрерывную и гладкую кривую точно через последовательность узловых точек, используя формулу, интерполяции Лагранжа:
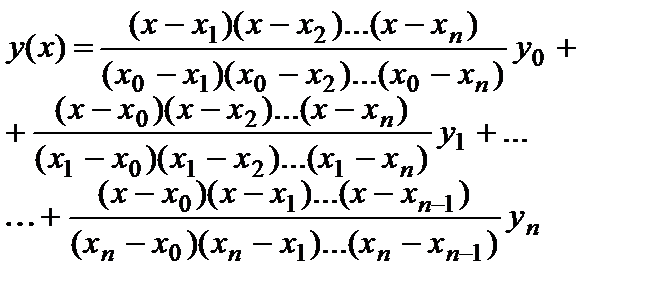
где 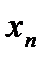 - значения аргумента в опорных точках траектории.
- значения аргумента в опорных точках траектории.
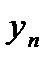 - значения функции в этих точках.
- значения функции в этих точках.
В этом случае мы получаем высокую плавность траектории, без каких либо скачков скорости и ускорения (см. рис.2.1), однако при этом методе степень полинома растет пропорционально числу точек, что увеличивает время расчетов и колебательность.
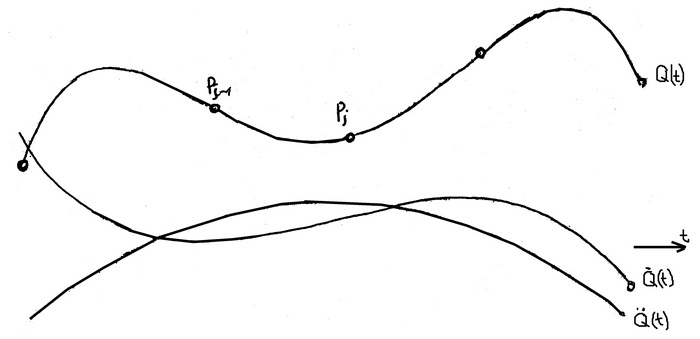
Рис. 2.1.Вид интерполяции по формуле Лагранжа
Кроме того, желаемую траекторию между узловыми точками очень трудно предугадать. По вышеперечисленным причинам метод интерполяции по формуле Лагранжа не нашел практического применения.
Четвертый этап решения - поточечное преобразование спланированной в обощенной системе координат траектории в систему декартовых координат путем решения прямой задачи кинематики. Прямую задачу будем решать геометрическим методом.
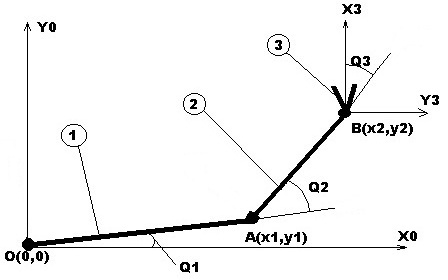
Рисунок 2.2.Решение ПЗК для манипулятора.
1.- первое звено; 2. -второе звено; 3. -третье звено (схват);
Декартовы координаты точек A(x1, y1) и B(x2, y 2) относительно центра базовой системы координат O(0, 0) вычисляются с помощью геометрических зависимостей (рис.2.3):
x1=l1cosQ1 ; x2=x1+l2cos(Q1+Q2);
y1=l1sinQ1; y2=y1+l2sin(Q1+Q2).
Таким образом, определили все необходимые для написания программы и моделирования движения манипулятора формулы.
|
|