
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Решение.Этот определитель вычислим по правилу диагоналей
|
|
Решение.Этот определитель вычислим по правилу диагоналей. Приписываем справа к определителю первый и второй столбцы. Перемножаем элементы, стоящие на главной диагонали и складываем это произведение с аналогичными произведениями элементов, стоящих на диагоналях, параллельных главной. Затем к произведению элементов, стоящих на побочной диагонали, прибавляем аналогичные произведения элементов, стоящих на диагоналях, параллельных побочной. Затем от первой суммы вычитаем вторую. Это и будет искомый определитель.
1       2 3 1 2
4 5 6 4 5
7 8 9 7 8 2 3 1 2
4 5 6 4 5
7 8 9 7 8
| 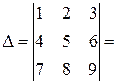
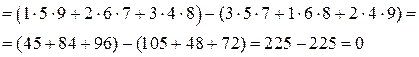
|
Ответ: 
б) 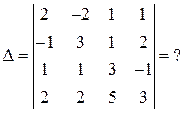
Решение. Решение найдем разложением по первому столбцу, но сначала с помощью свойств определителя сделаем нули в этом столбце везде кроме элемента, равного минус единице.
Для этого элементы второй строки умножим на два и прибавим к соответствующим элементам первой строки; элементы второй строки прибавим к соответствующим элементам третьей строки; элементы второй строки умножим на два и прибавим к соответствующим элементам четвертой строки. Эти действия записываем так:

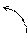
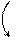
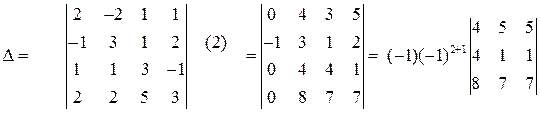 .
.
Разложив определитель 4-го порядка по 1-му столбцу, свели его вычисление к нахождению одного определителя 3-го порядка, который можно вычислить по правилу диагоналей, разобранному выше. Можно дальше применить свойства определителя и свести этот определитель к одному определителю 2-го порядка. Продолжаем делать нули теперь уже во второй строке, умножая элементы третьего столбца на 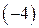 и прибавляя к первому и второму столбцам:
и прибавляя к первому и второму столбцам:



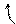
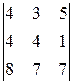 =
= 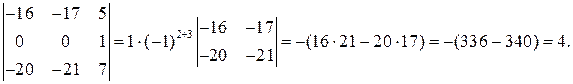
(-4)
(-4)
Ответ: 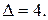
2) Умножить матрицы:



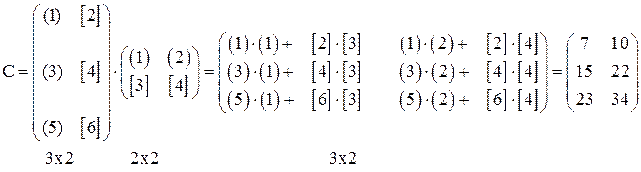 .
.
Решение. Произведение матриц получили, умножая элементы строк первой матрицы на соответствующие элементы столбцов второй матрицы и складывая их.
Ответ: 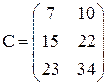 .
.
3) Найти обратные матрицы:
а) 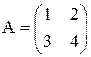
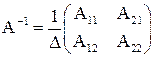 .
.
Решение. Сначала находим 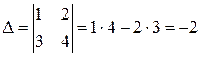 ;
;  , значит, существует матрица
, значит, существует матрица 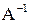 . Находим алгебраические дополнения:
. Находим алгебраические дополнения:






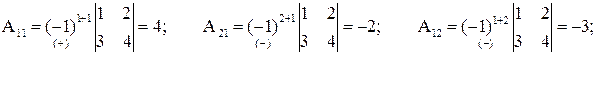
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение


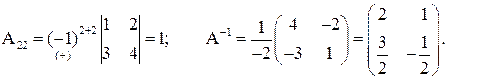
Ответ: 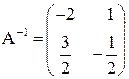 .
.
4) Найти двумя способами ранг матрицы:  .
.
Решение.
1 способ. Метод окаймляющих миноров. Находим любой минор второго по
рядка, отличный от нуля, например 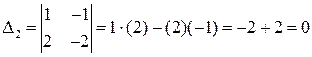 , по-
, по-
этому выписываем другой определитель 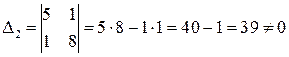 . Нашелся определитель второго порядка, отличный от нуля, значит ранг
. Нашелся определитель второго порядка, отличный от нуля, значит ранг 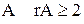 . Теперь найдем определитель третьего порядка, окаймляющий найденный
. Теперь найдем определитель третьего порядка, окаймляющий найденный 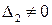 .
.



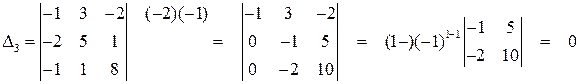
Берем другой определитель, окаймляющий 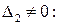


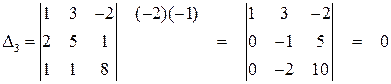 , как и предыдущий.
, как и предыдущий.
Больше окаймляющих миноров третьего порядка для 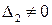 нет, поэтому ранг А, равный наивысшему порядку минора, отличного от нуля, равен двум.
нет, поэтому ранг А, равный наивысшему порядку минора, отличного от нуля, равен двум.
|
|
