Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Проведение экстраполяции

В математике экстраполяцией называется предсказание поведения некоторой зависимости по имеющимся измерениям ее характеристики в определенной, иногда довольно узкой области.

В MathCAD экстраполяция основывается на анализе поведения зависимости в нескольких точках.

Функцией, реализующей алгоритм линейной экстраполяции является встроенная функция

predict (y, m, n),

где y – вектор эмпирических значений экстраполируемой характеристики по оси ординат. Особенность алгоритма, используемого функцией, заключается в том, что экстраполяцию он делает только на основании y -координат выборки при постоянном шаге по оси абсцисс;

m – количество ближайших к правой границе выборки точек, на основании которых проводится экстраполяция;

n – количество точек в просчитываемом векторе прогноза.

При помощи функции «predict» можно проводить довольно эффективную экстраполяцию непрерывных, периодических или осциллирующих функций в относительно неширокой области.

Выполнить пример:

Предсказать поведение кривой затухающих колебаний.

Для этого зададим вектор из y-координат его 101-ой точкой на промежутке от 0 до 3 π. Шаг изменения переменной при определении вектора данных должен быть постоянным. Организуем вектор путем использования ранжированных переменных.

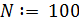
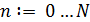
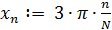
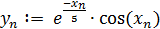
Далее зададим векторы экстраполяции при помощи функции «predict».

Чтобы сравнить степень влияния количества анализируемых точек выборки на качество предсказания, определим три экстраполяционных вектора при различных значениях параметра m. Размерность этих векторов определим, например, 150.

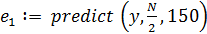
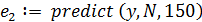
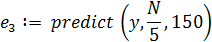
Строим графики векторов приближений (рис. 6.39).

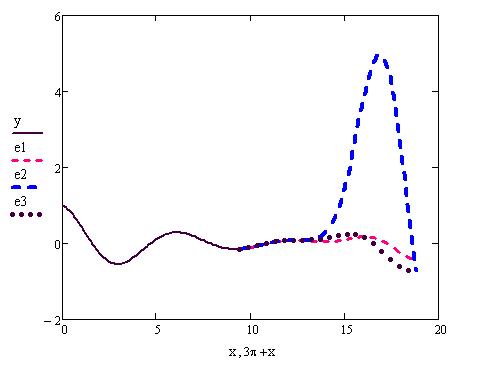
Рис. 6.39 Графики векторов приближений

При этом переменная для векторов экстраполяции может быть определена прибавлением к вектору x соответствующей координаты крайнего значения в выборке (3π).

5.5 Контрольные вопросы

- дать понятие о кусочно-линейной интерполяции.

- дать понятие о сплайновой интерполяции.

- какая функция используется для выполнения кусочно-линейной интерполяции.

- пояснить этапы проведения сплайн-аппроксимации.