Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Ситуационная (практическая) задача № 2

При измерении веса 25 упаковок сильнодействующего лекарственного препарата были обнаружены следующие отклонения (в гр.) от указанного на обертке:

–24, 34; –14, 59; –18, 27; –8, 94; –15, 09; –10, 94; 4, 47; 3, 05; –8, 33; –22, 98; 1, 75;

–32, 07; –7, 43; –18, 63; –12, 97; –11, 08; –7, 44; –1, 70; 6, 34; –11, 08; –11, 12; –15, 90;

–10, 26; –8, 07; –6, 48.

Необходимо:

§ Определить исследуемый признак и его тип (дискретный или непрерывный).

§ В зависимости от типа признака построить полигон или гистограмму относительных частот.

§ На основе визуального анализа полигона (гистограммы) сформулировать гипотезу о законе распределения признака.

§ Вычислить выборочные характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое (стандартное) отклонение.

§ Используя критерий согласия «хи-квадрат» Пирсона, проверить соответствие выборочных данных выдвинутому в п.3 закону распределения при уровне значимости 0, 05.

§ Для генеральной средней и дисперсии построить доверительные интервалы, соответствующие доверительной вероятности 0, 95.

§ С надежностью 0, 95 проверить гипотезу о равенстве:

а) генеральной средней значению –10;

б) генеральной дисперсии значению 100.

Решение:

1. Тип признака непрерывный, т.к. исходные цифры могут принимать любые дробные значения на определенном промежутке.

Разобьем данные на 5 равных интервалов:

Длина интервала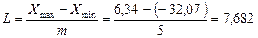

Интервал

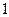
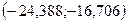
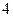
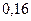
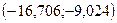
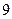
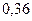
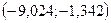
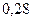
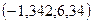
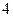
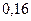
Гистограмма относительных частот

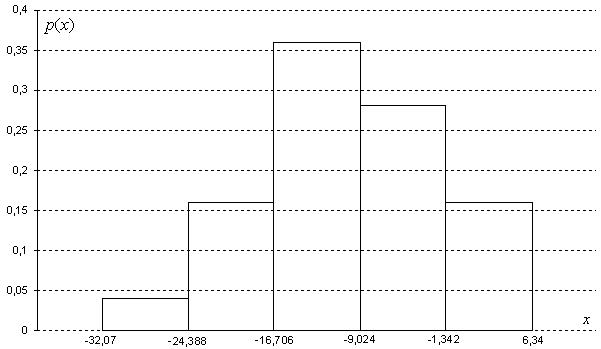
3. На основе анализа гистограммы распределения выдвигаем гипотезу о нормальном законе распределения исследуемого признака.

4. Среднее значение:

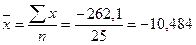
Дисперсия:

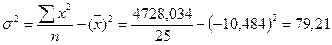
Среднее квадратическое (стандартное) отклонение:

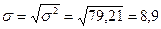
5. Вводим гипотезы:

Исследуемый признак имеет нормальное распределение:

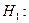Исследуемый признак имеет другое распределение:

Условие принятия гипотезы

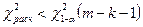
Вероятность попадания в интервалы:

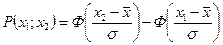
Интервал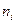
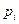
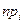
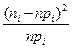
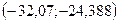
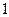
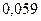
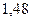
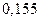
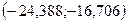
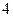
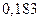
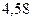
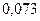
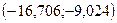
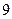
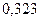
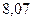
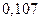
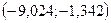
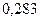
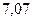
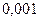
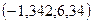
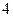
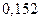
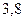
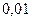
Сумма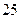

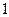
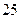
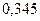
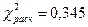
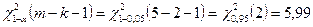
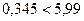, следует гипотезу о нормальном распределении исследуемого признака принимаем, при доверительной вероятности 95%.

6. Доверительный интервал для генерального среднего, при доверительной вероятности 95%:

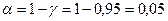
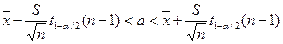
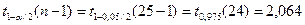
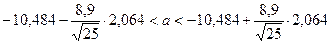
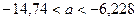
С вероятностью 95% генеральное среднее находится в интервале от до .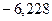

Доверительный интервал для генеральной дисперсии, при доверительной вероятности 95%:

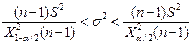
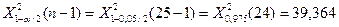
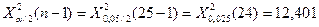
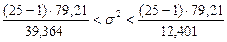
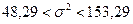
С вероятностью 95% генеральная дисперсия находится в интервале от 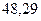до .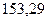

7а. Вводим гипотезы:

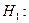
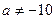
Условие принятия гипотезы

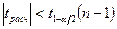
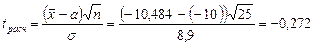
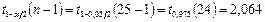
Условие принятия гипотезы выполняется 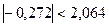, следует с вероятностью 95% генеральное среднее можно считать равным -10.

7б. Вводим гипотезы:

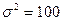
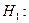
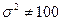
Условие принятия гипотезы

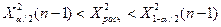
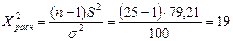
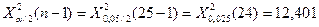
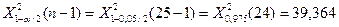
Условие принятия гипотезы выполняется 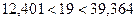, следует с вероятностью 95% генеральную дисперсию можно считать равной 100.