
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Порядок виконання завдання
|
|
Дослідимо наявність мультиколінеарності, виконавши такі кроки:
1. Нормалізацію (стандартизацію) пояснювальних змінних моделі.
2. Розрахунок кореляційної матриці rхх.
3. Визначення детермінанта матриці rхх. та критерію c2.
4. Розрахунок матриці, оберненої до матриці rхх.
5. Визначення F-критерію.
6. Обчислення частинних коефіцієнтів кореляції.
7. Визначення t-критерію.
Крок 1. Нормалізація (стандартизація) незалежних змінних моделі.
Обчислимо середні арифметичні незалежних змінних:
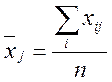
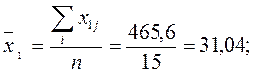
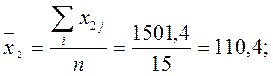
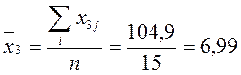 .
.
Визначимо стандартні відхилення.
Позначимо вектори незалежних змінних – продуктивності праці, фондомісткості, коефіцієнтів плинності робочої сили – через Х1, Х2, Х3. Елементи нормалізованих векторів обчислимо за формулою:
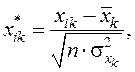
де n – кількість спостережень, n = 15;
m – кількість незалежних змінних, m = 3;
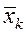 – середнє арифметичне значення компонентів вектора х k;
– середнє арифметичне значення компонентів вектора х k;
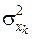 – дисперсія змінної х k.
– дисперсія змінної х k.
Із формули випливає, що спочатку потрібно обчислити середні арифметичні значення і величини 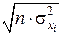 для кожної незалежної змінної. Дисперсії кожної незалежної змінної мають такі значення:
для кожної незалежної змінної. Дисперсії кожної незалежної змінної мають такі значення:
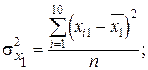
| 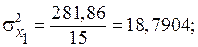
|
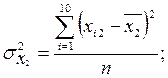
| 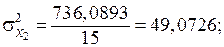
|
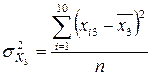
| 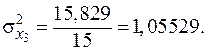
|
Усі розрахункові дані для нормалізації змінних Х1, Х2, X3, згідно з поданими співвідношеннями наведено в табл. 7.4.
Таблиця 8.4
| 
| 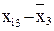
| 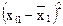
| 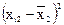
| 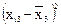
| 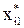
| 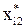
| 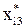
|
| –7, 94 | –9, 79 | –1, 39 | 63, 0436 | 95, 9094 | 1, 9414 | –0, 4729 | –0, 3610 | –0, 3502 |
| –6, 04 | –7, 49 | –1, 19 | 36, 4816 | 56, 1500 | 1, 4240 | –0, 3598 | –0, 2762 | –0, 2999 |
| –4, 04 | –6, 59 | –0, 99 | 16, 3216 | 43, 4720 | 0, 9867 | –0, 2406 | –0, 2430 | –0, 2497 |
| –2, 34 | –6, 29 | –0, 89 | 5, 4756 | 39, 6060 | 0, 7980 | –0, 1394 | –0, 2320 | –0, 2245 |
| –1, 24 | –4, 89 | –0, 79 | 1, 5376 | 23, 9447 | 0, 6294 | –0, 0739 | –0, 1804 | –0, 1994 |
| –0, 74 | –2, 19 | –0, 69 | 0, 5476 | 4, 8107 | 0, 4807 | –0, 0441 | –0, 0808 | –0, 1743 |
| –0, 74 | –1, 79 | –0, 39 | 0, 5476 | 3, 2160 | 0, 1547 | –0, 0441 | –0, 0661 | –0, 0989 |
| –0, 64 | –1, 09 | –0, 29 | 0, 4096 | 1, 1954 | 0, 0860 | –0, 0381 | –0, 0403 | –0, 0737 |
| –0, 54 | 1, 01 | –0, 19 | 0, 2916 | 1, 0134 | 0, 0374 | –0, 0322 | 0, 0371 | –0, 0486 |
| –0, 24 | 1, 71 | 0, 21 | 0, 0576 | 2, 9127 | 0, 0427 | –0, 0143 | 0, 0629 | 0, 0519 |
| 0, 96 | 2, 11 | 0, 91 | 0, 9216 | 4, 4380 | 0, 8220 | 0, 0572 | 0, 0776 | 0, 2279 |
| 2, 86 | 2, 91 | 1, 11 | 8, 1796 | 8, 4487 | 1, 2247 | 0, 1704 | 0, 1071 | 0, 2782 |
| 5, 16 | 4, 21 | 1, 31 | 26, 6256 | 17, 6960 | 1, 7074 | 0, 3074 | 0, 1551 | 0, 3284 |
| 7, 06 | 9, 91 | 1, 61 | 49, 8436 | 98, 1420 | 2, 5814 | 0, 4205 | 0, 3651 | 0, 4038 |
| 8, 46 | 18, 31 | 1, 71 | 71, 5716 | 335, 1340 | 2, 9127 | 0, 5039 | 0, 6748 | 0, 4290 |
| Всього… | 281, 86 | 736, 0893 | 15, 829 |
Тоді знаменник для нормалізації кожної незалежної змінної буде такий:
X1: 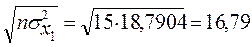 ;
;
X2: 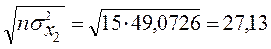 ;
;
X3: 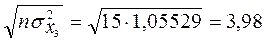 .
.
Матриця нормалізованих змінних подається у вигляді:
| –0, 4729 | –0, 3610 | –0, 3502 | |
| –0, 3598 | –0, 2762 | –0, 2999 | |
| –0, 2406 | –0, 2430 | –0, 2497 | |
| –0, 1394 | –0, 2320 | –0, 2245 | |
| –0, 0739 | –0, 1804 | –0, 1994 | |
| –0, 0441 | –0, 0808 | –0, 1743 | |
| –0, 0441 | –0, 0661 | –0, 0989 | |
| Х* = | –0, 0381 | –0, 0403 | –0, 0737 |
| –0, 0322 | 0, 0371 | –0, 0486 | |
| –0, 0143 | 0, 0629 | 0, 0519 | |
| 0, 0572 | 0, 0776 | 0, 2279 | |
| 0, 1704 | 0, 1071 | 0, 2782 | |
| 0, 3074 | 0, 1551 | 0, 3284 | |
| 0, 4205 | 0, 3651 | 0, 4038 | |
| 0, 5039 | 0, 6748 | 0, 4290 |
Крок 2. Розрахунок кореляційної матриці нульового порядку).
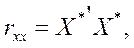
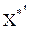 де X* – матриця нормалізованих пояснювальних змінних;
де X* – матриця нормалізованих пояснювальних змінних;
– матриця, транспонована до X*.
Маємо:
| –0, 4729 | –0, 3610 | –0, 3502 | |
| –0, 3598 | –0, 2762 | –0, 2999 | |
| –0, 2406 | –0, 2430 | –0, 2497 | |
| –0, 1394 | –0, 2320 | –0, 2245 | |
| –0, 0739 | –0, 1804 | –0, 1994 | |
| –0, 0441 | –0, 0808 | –0, 1743 | |
| –0, 0441 | –0, 0661 | –0, 0989 | |
| Х* = | –0, 0381 | –0, 0403 | –0, 0737 |
| –0, 0322 | 0, 0371 | –0, 0486 | |
| –0, 0143 | 0, 0629 | 0, 0519 | |
| 0, 0572 | 0, 0776 | 0, 2279 | |
| 0, 1704 | 0, 1071 | 0, 2782 | |
| 0, 3074 | 0, 1551 | 0, 3284 | |
| 0, 4205 | 0, 3651 | 0, 4038 | |
| 0, 5039 | 0, 6748 | 0, 4290 |
| –0, 47294 | –0, 35977 | –0, 24064 | –0, 13938 | –0, 07386 | –0, 04408 | –0, 04408 | –0, 03812 | ||||
| X*' = | –0, 36097 | –0, 27619 | –0, 24302 | –0, 23196 | –0, 18036 | –0, 08084 | –0, 0661 | –0, 0403 | |||
| –0, 35021 | –0, 29994 | –0, 24967 | –0, 22453 | –0, 1994 | –0, 17427 | –0, 09886 | –0, 07373 | ||||
| Продовження матриці | |||||||||||
| –0, 03216 | –0, 0143 | 0, 057182 | 0, 170354 | 0, 307352 | 0, 420524 | 0, 503914 | |||||
| 0, 03710 | 0, 062905 | 0, 077648 | 0, 107135 | 0, 15505 | 0, 365142 | 0, 674752 | |||||
| –0, 04859 | 0, 051944 | 0, 227885 | 0, 278154 | 0, 328423 | 0, 403826 | 0, 428961 | |||||
| 0, 9440 | 0, 9426 | ||
| rxx = | 0, 9440 | 0, 9183 | |
| 0, 9426 | 0, 9183 |
Кожний елемент цієї матриці характеризує тісноту зв'язку однієї незалежної змінної з іншою. Оскільки діагональні елементи характеризують тісноту зв'язку кожної незалежної з цією самою змінною, то вони дорівнюють одиниці.
Решта елементів матриці rхх такі:
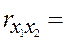
| 0, 944; |
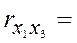
| 0, 9426; |
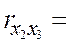
| 0, 9183. |
Парні коефіцієнти кореляції характеризують тісноту зв'язку між двома змінними. Вони можуть змінюватися в межах
від –1 до 1.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Коефіцієнти парної кореляції r12, r13 близькі до одиниці, тому можна передбачити, що досліджувані незалежні змінні є мультиколінеарними. Користуючись цими коефіцієнтами, можна зробити висновок, що між змінними Х1 і Х2, Х1 і Х3 та Х2 і Х3 існує вельми високий зв'язок.
Постає запитання: чи цей зв’язок є виявленням мультиколінеарності і через це негативно впливатиме на оцінку параметрів економетричної моделі? Звертаємося до алгоритму Фаррара-Глобера.
Крок 3. Обчислимо детермінант кореляційної матриці rхх і критерій c2:
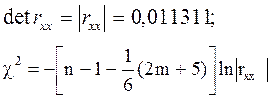 а)
а)
б) (n=15; m=3)
ln|rxx | = –4, 482;
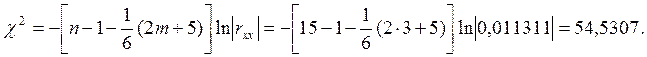
Отже, критерій c2= 54, 5307.
Якщо ступінь свободи дорівнює 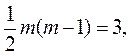 а рівень значущості a=0, 01, то критерій c2табл = 11, 3449.
а рівень значущості a=0, 01, то критерій c2табл = 11, 3449.
Оскільки 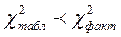 – робимо висновок, що в масиві змінних існує мультиколінеарний зв'язок.
– робимо висновок, що в масиві змінних існує мультиколінеарний зв'язок.
Крок 4. Розрахуємо матрицю, обернену до матриці rxx:
| 13, 85 | –6, 93 | –6, 69 | |
| C = | –6, 929 | 9, 85 | –2, 51 |
| –6, 691 | –2, 51 | 9, 62 |
Матриця C – симетрична, і її діагональні елементи завжди мають бути додатними.
Крок 5. Визначення F-критерію:
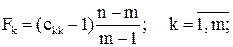 |
де n – кількість спостережень; m – кількість пояснювальних змінних.
Виконавши обчислення, дістанемо:
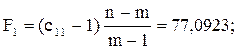
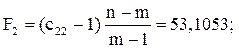
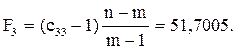
Коли a = 0, 05 і ступені свободи m–1=3–1=2, n–m=15–3=12 маємо Fкрит = 3, 885.
Фактично знайдене значення F-критерію порівнюємо з табличним. У нашому випадку Fфакт > Fкрит , тобто незалежні змінні мультиколінеарні з рештою змінних.
Коефіцієнт детермінації до кожної змінної:
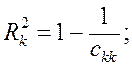
| R21 = | 0, 9278; | R22 = | 0, 898; | R23 = | 0, 896. |
Якщо коефіцієнт детермінації наближається до одиниці, то незалежна змінна мультиколінеарна з іншими.
Крок 6. Обчислення частинних коефіцієнтів кореляції:
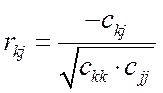
де сkj – елемент матриці С, що міститься в k-му рядку i j-му стовпці;
сkk і сjj – діагональні елементи матриці С.
| r12 = | 0, 5932; |
| r13 = | 0, 5798; |
| r23 = | 0, 5284. |
Частинні коефіцієнти кореляції характеризують рівень тісноти зв'язку між двома змінними за умови, що решта змінних на цей зв'язок не впливає. Частинні коефіцієнти кореляції за модулем нижчі, ніж коефіцієнти парної кореляції, бо на їхній рівень не впливає решта змінних, які мають зв'язок із цими двома.
Крок 7. Обчислення t-критеріїв:
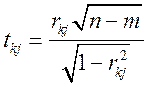

| t12 = 2, 553 |
| t13 = 2, 465 |
| t23 = 0, 926 |
| tкрит = 2, 179 |
Обчислені t-критерії порівнюємо з табличним за вибраного рівня значущості a = 0, 05 і ступенів свободи n–m= 12.
Якщо tkj більше за tтабл, як у нашому випадку, то пара цих пояснювальних змінних тісно пов'язана між собою.
Оскільки розраховані t12 > tтабл та t13 > tтабл, то можна зробити висновок, що пари цих пояснювальних змінних (X1 і X2 та X1 і X3) – тісно пов'язані між собою.
|
|
