
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Параметры, определяемые с помощь ИНС. Бесплатформенные ИНС.
|
|
Параметры, определяемые с помощью ИНС. Инерциальные системы предназначены для определения координат места самолета. Но в процессе их определения можно получить значения многих других параметров, необходимых для навигации. Перечислим основные из этих параметров и рассмотрим, каким образом они могут быть получены.
1. Курс, крен и тангаж. Это параметры, определяющие угловое положение самолета относительно трех осей. В традиционных ИНС гироплатформа стабилизирована по меридиану и в горизонтальной плоскости, поэтому не составляет труда определить угловое положение ВС относительно гироплатформы, то есть три перечисленных параметра. В бесплатформенных системах эти параметры рассчитываются путем интегрирования угловых скоростей.
ИНС непосредственно измеряет истинный курс, то есть курс относительно текущего географического меридиана. Но, поскольку текущие счисленные координаты всегда известны, вычислитель ИНС (или центральный вычислитель навигационного комплекса самолета) может рассчитать и ортодромический курс относительно любого опорного направления.
В памяти современных ИНС хранится модель магнитного поля Земли, с помощью которой вычислитель может рассчитать магнитное склонение в точке расположения самолета. Тогда система может определить и магнитный курс, вычтя магнитное склонение из измеренного истинного курса.
У современных БИНС погрешности определения крена и тангажа составляют 0, 05-0, 1°, а истинного курса около 0, 4°. Погрешность определения магнитного курса зависит еще и от точности модели магнитного поля и составляет порядка 1-1, 5°.
2. Угловые скорости изменения курса, крена, тангажа. В бесплатформенных системах эти параметры непосредственно измеряются лазерными гироскопами (с погрешностью порядка 0, 1º в секунду), а в традиционных ИНС при необходимости могут быть получены расчетным путем.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
3. Ускорения самолета по трем перпендикулярным осям. В традиционных ИНС ускорения измеряются по осям земной системы координат (на север, на восток, вверх), а в БИНС – по строительным осям ВС (вперед, вправо, вверх) и затем пересчитываются в земную систему координат. Значения ускорений нигде не индицируются, а только используются для дальнейших расчетов.
4. Скорости перемещения ВС по трем осям земной системы координат: на север WN, на восток WE, вверх Wверт. Разумеется, скорости, как и ускорения могут быть фактически быть направлены и на юг, запад, вниз – это отразится в знаке перечисленных скоростей. Погрешности определения горизонтальных составляющих скорости составляют единицы километров в час, а вертикальной скорости порядка 0, 2 м/с.
5. Путевая скорость W. Поскольку составляющие путевой скорости известны, то и путевая скорость (рис. 8.28) может быть определена по формуле:
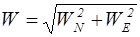 .
.
6. Фактический путевой угол β Ф. Фактический истинный путевой угол (см. рис. 8.28), может быть определен по формуле:
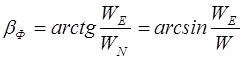 .
.
Путем вычитания магнитного склонения может быть получен и магнитный путевой угол.
7. Угол сноса α. Поскольку фактический путевой угол β Ф и курс γ известны, то в соответствии с навигационным треугольником скоростей
α = β Ф – γ.
8. Географические координаты места самолета. В простейшем случае, если принять Землю за сферу, то по составляющим путевой скорости могут быть рассчитаны сферические широта φ и долгота λ места самолета по формулам (8.6). В вычислителе может быть запрограммирован алгоритм учета поправок в координаты за счет сжатия Земли или алгоритм расчета координат на поверхности земного эллипсоида. Возможно, в этом и нет особой необходимости. Ведь требуемая международными документами точность определения счисленных координат с помощью ИНС, которая и реализована в современных системах, составляет 1 морскую милю (1, 852 км) за час полета, а поправки за счет сжатия Земли имеют гораздо меньшую величину.
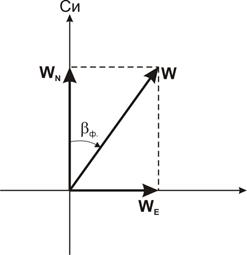
Рис. 8.28. К определению W и ФПУ
9. Высота полета. Высота является третьей пространственной координатой и, как и горизонтальные координаты (φ и λ), может быть рассчитана с помощью ускорения, измеряемого вертикальным акселерометром. Полученная таким образом высота, называемая иногда инерциальной высотой, имеет такой же порядок точности как и горизонтальные координаты. Разумеется, для высоты это совершенно неудовлетворительная точность и поэтому инерциальная высота пока не используется в навигации ни для эшелонирования, ни для предотвращения столкновений с препятствиями. Но она может использоваться в алгоритмах работы самой ИНС. Например, для расчета радиуса Земли с учетом высоты полета, необходимого для определения положения текущей горизонтальной плоскости.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Можно видеть, что перечисленный список определяемых ИНС параметров включает в себя почти все величины, необходимые для навигации. Тем не менее, ИНС самостоятельно не может определить, например, скорость и направление ветра, поскольку для этого необходимо знать еще и истинную воздушную скорость, которую система не измеряет. Для расширения возможностей современных ИНС на вход их вычислителей подается информация от других бортовых систем. Например, от системы воздушных сигналов может поступать истинная воздушная скорость и барометрическая высота. В этом случае возможно и определение ветра.
Вычислитель, входящий в состав ИНС, предназначен для решения своих специфических задач: определения счисленных координат и других параметров. Он имеет и необходимую для своей работы память. Но почему бы не «загрузить» этот вычислитель и память дополнительными функциями, полезными для навигации?
Даже первые образцы используемых в гражданской авиации ИНС имели возможность ввести в память географические координаты нескольких ППМ. Тогда появляется возможность определения еще целого ряда параметров. Например, следующих:
- з аданного путевого угла и длины участка маршрута. Поскольку координаты начального и конечного ППМ каждого участка маршрута известны, можно математически рассчитать длину и направление ортодромической ЛЗП;
- линейного бокового уклонения и оставшегося до ППМ расстояния. Эта задача тоже решается чисто математически, поскольку координаты ВС и ППМ участка известны;
- оставшегося времени полета до ППМ и гринвичского времени его пролета;
- поправки в фактический путевой угол для выхода в ППМ,
а также других параметров. Разумеется, не во всех ИНС эти функции реализованы в полном объеме. В них нет необходимости, если эти же задачи решает центральный вычислитель навигационного комплекса, в который входит ИНС как один из датчиков.
|
|
