Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Приложение 1. Магнитное поле катушек Гельмгольца

Рассмотрим круговой виток из тонкого провода радиуса R, по которому циркулирует ток I. Вычислим магнитную индукцию на оси этого витка на расстоянии z от него (см. рис.8). Для этого разобьём виток на бесконечно малые элементы тока 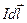. По закону Био-Савара каждый такой элемент создаёт поле

.

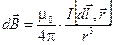Как видно на рис.9, вектора 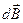от различных элементов образуют конус, и результирующий вектор 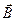в точке A направлен вверх по оси Z. Вычислив проекцию 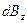и проинтегрировав по dl, получаем:

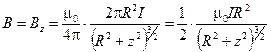. (6)

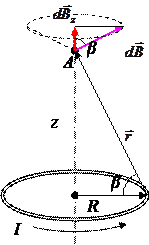
Рис.8. К выводу формулы для магнитного поля на оси кругового тока.

Применим полученный результат к кольцам Гельмгольца, изображённым на Рис.9. В точке, равноудаленной от колец, их вклады в магнитное поле равны по модулю и по направлению, поэтому магнитную индукцию (6) необходимо удвоить. Подставляя 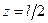, получим:

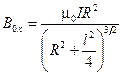. (7)

При l = R получаем

.

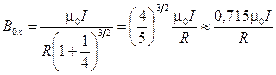Для случая N витков в каждой катушке имеем

.

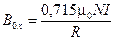Это выражение совпадает с формулой (5).

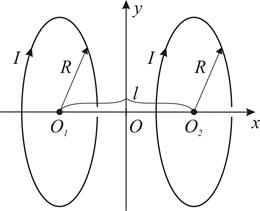
Рис.9. Параллельные круговые витки с током.

В точках с координатами (x, y), отличными от нуля, компоненты магнитного поля выражаются формулами (4). Если сравнить их с формулой (5), то можно сделать вывод, что в качестве критерия однородности удобно выбрать величины:

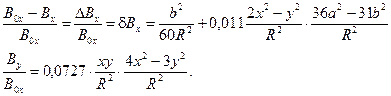(8)

Первое выражение в (8) описывает отклонение величины магнитного поля от формулы (5) по абсолютной величине, а второе – позволяет учесть отклонение магнитного поля от оси X. В областях пространства, где определяемые (8) поправки составляют менее 1%, магнитное поле можно считать однородным.