Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Теоретическая часть. Определение удельного заряда электрона

Лабораторная работа № 11

Определение удельного заряда электрона

Цель работы: определение удельного заряда электрона по траектории пучка электронов в магнитном поле.

Теоретическая часть

Удельный заряд элементарной частицы, равный отношению ее электрического заряда к массе, является одной из её важнейших характеристик. Знание этой величины позволяет, например, идентифицировать частицы по их трекам в регистрирующих устройствах. Один из методов нахождения удельного заряда – определение радиуса кривизны траектории движения частицы в магнитном поле.

На заряженную частицу с зарядом 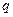, движущуюся со скоростью 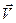в магнитном поле с индукцией 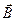, действует сила Лоренца:

.

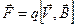В неоднородном поле траектория движения представляет собой винтовую линию переменного радиуса и шага. Однако, если частица движется в однородном магнитном поле, и вектор скорости 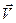перпендикулярен вектору магнитной индукции 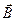, то траектория движения становится проще – она превращается в окружность, плоскость которой перпендикулярна вектору 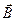. Радиус окружности 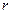можно найти с помощью второго закона Ньютона:

,

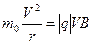где 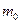– масса частицы, q – ее заряд, 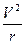– центростремительное ускорение частицы. Отсюда следует, что

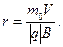(1)

Первоначально покоившаяся частица, попадающая в магнитное поле после прохождения в электрическом поле ускоряющей разности потенциалов U, приобретает кинетическую энергию

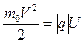. (2)

Приведенные соотношения (1) и (2) справедливы в нерелятивистском приближении. Исключив из них скорость, для электрона получим

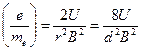, (3)

где 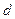- диаметр окружности.

Таким образом, зная радиус r (или диаметр d) круговой траектории движения электрона в магнитном поле с известной индукцией B, а также ускоряющую разность потенциалов U, можно вычислить отношение величины заряда электрона e к его массе m_e, т.е. величину удельного заряда электрона.