
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Диференційне рівняння теплопровідності.
|
|
Для розв’язку задач, пов’язаних з визначенням температурного поля як функції координати та часу необхідно мати диференційне рівняння теплопровідності. В загальному вигляді для тривимірного простору за відсутності внутрішніх джерел та стоків теплоти диференційне рівняння має вигляд
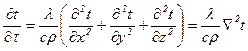 , (15)
, (15)
де 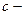 теплоємність матеріалу,
теплоємність матеріалу, 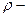 густина матеріалу,
густина матеріалу, 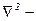 оператор Лапласа. Ліва частина цього рівняння (
оператор Лапласа. Ліва частина цього рівняння ( ) це швидкість зміни температури, права – (
) це швидкість зміни температури, права – (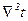 ) це швидкість зміни градієнта температури.
) це швидкість зміни градієнта температури.
Якщо значення коефіцієнта теплопровідності, густини та теплоємності мало змінюються при зміні температури – можна застосувати коефіцієнт температуропровідності матеріалу 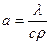 .
.
Величина температуропровідності є мірою того, як швидко відбувається вирівнювання температурного поля. Тіло з більшою температуропровідністю нагрівається або охолоджується скоріше. Коефіцієнт температуропровідності має розмірність м2/с.
Загалом диференційне рівняння теплопровідності можна прочитити як: швидкість зміни температури тіла за проміжок часу пропорційна його температуропровідності.
У випадку одновимірної задачі 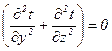 і диференційне рівняння теплопровідності набуває вигляду
і диференційне рівняння теплопровідності набуває вигляду
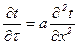 . (16)
. (16)
Диференційні рівняння теплопровідності встановлюють зв’язок між часовою та просторовою зміною температури всередині тіла. Для того, щоб знайти температурне поле всередині тіла в будь який момент часу (тобто щоб розв’язати диференційне рівняння) необхідно знати розподіл температур в початковий момент часу (початкова умова), геометричну форму тіла і закон взаємодії між оточуючим середовищем і поверхнею тіла (граничні умови).
В загальному вигляді аналітичним рішенням рівняння (16) є вираз
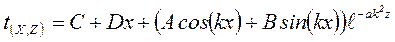 , (17)
, (17)
де C, D, A, k, B – постійні коефіцієнти, що залежать від часових та граничних умов. Часові умови бувають двох видів: початкові та кінцеві. Кінцеві умови визначають розподіл температур в тілі після закінчення нескінченого проміжку часу (тобто в стаціонарному тепловому режимі).
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Граничні умови визначають характер теплообміну на поверхні теплопередаючого матеріалу. Відповідно кількість граничних умов рівна кількості поверхонь. Якщо біля всіх поверхонь однакові граничні умови то кажуть, що вини симетричні, якщо різні – несиметричні. Існує чотири види головних граничних умов:
– постійна температура на поверхні (обмурівка доменної печі – рідкий метал);
– постійний тепловий потік на поверхні (результат інфрачервоного опромінення поверхні);
– постійний коефіцієнт теплообміну (метал-повітря);
– умова ідеального контакту між сусідніми поверхнями (багатошарова стінка).
В деяких випадках всередині твердого тіла може виділятися або поглинатися теплова енергія (фільтрація повітря, випаровування вологи. адсорбція та десорбція…). Виділення теплової енергії вважається позитивним джерелом теплоти, поглинання теплової енергії вважається негативним джерелом теплоти. Якщо відома питома теплова потужність джерела теплоти W, Вт/м3 диференційне рівняння має вигляд
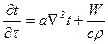 . (18)
. (18)
|
|
