Ошибки в научных вычислениях

💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Если результаты вычислений с плавающей точкой отличается от ожидаемых, налицо ошибка. Ошибки могут возникать по ряду причин:

3. Ошибки эксперимента: данные получены с помощью средств ограниченной точности, например, измерительных инструментов, либо эксперимент некорректно поставлен для конкретной задачи.

4. Игнорирование существенных особенностей задачи. Например, если в качестве приближения для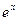

взять, скажем, сумму первых пяти членов соответствующего ряда Тейлора, то, независимо от точности вычислений и используемого компьютера, неизбежна некоторая ошибка за счет использования усеченной суммы ряда.

6. Неустойчивость используемого для решения задачи алгоритма.

7. чувствительность решаемой задачи к погрешностям.

1. Чем «ручные» вычисления отличаются от машинной арифметики?

2. Чем определяется система чисел с плавающей точкой?

3. Основные отличия множества чисел с плавающей точкой от множества действительных чисел.

4. За счет чего в системе чисел с плавающей точкой происходит нарушение законов классической арифметики? К чему это приводит?

5. Представление чисел в ЭВМ. Что такое мантисса числа? Какая система называется нормализованной?

6. Представить числа в нормализованной системе с плавающей точкой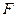

, для которой

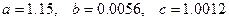7. Какие ситуации могут возникнуть при представлении числа в ЭВМ? Их последствия.

8. Что такое округление, усечение числа при его представлении в системе с плавающей точкой? Какой способ приближения является более точным, на сколько? Почему? Привести примеры.

9. Что представляет из себя машинное эпсилоном?

10. Устойчивость и неустойчивость алгоритма. Привести примеры. Можно ли неустойчивый алгоритм сделать устойчивым?

11. Чувствительные и нечувствительные задачи. Примеры. Можно ли устранить чувствительность задачи?

1. Каханер Д. Численные методы и программное обеспечение / Д.Каханер, К.Моулер, С.Нэш; пер. с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 575 с.

2. Бахвалов Н.С. Численные методы / Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. — М.: БИНОМ. Лаборатория знаний, 2006. — 636 с.