💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Представление чисел в ЭВМ

В машинных вычислениях участвуют числа двух типов: целые и вещественные («с плавающей точкой»). Первые компьютеры допускали только целочисленную арифметику. Для представления дробей использовалась воображаемая точка в фиксированной позиции внутри целого числа. Это называлось «арифметикой с фиксированной точкой». В 1954 г. фирма IBM начала производство компьютера 704, в котором все алгоритмы для вещественных чисел были реализованы как машинные команды, что чрезвычайно упрощало использование нецелочисленной арифметики. Арифметика с фиксированной точкой более не является стандартным режимом компьютера, исключение составляют лишь некоторые специализированные устройства. Стандартна аппаратно реализованная арифметика с плавающей точкой.

Множество чисел с плавающей точкой 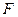характеризуется 4-мя параметрами: числом разрядов 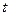, основанием системы счисления 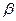, границами изменения показателя. Каждое число 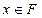представляется в виде:

,

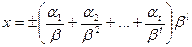где 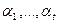- целые числа такие, что , а 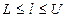. Число 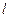называется показателем, 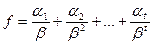- дробной частью или мантиссой.

Если для любого ненулевого числа 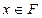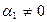, то система называется нормализованной.

Множество 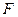является конечным, а значит имеет наибольший и наименьший по модулю элементы в отличие от множества действительных чисел 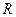. Числа, меньшие по модулю минимального ненулевого числа из множества 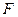, представляются в ЭВМ нулем. Минимальное положительное число , которое может быть представлено в системе с плавающей точкой 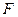, иногда называется машинным нулем.

В силу конечности множества 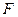при представлении заданного ненулевого числа 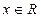в системе чисел с плавающей точкой могут возникнуть 4 ситуации:

1) число 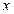по модулю больше максимального из чисел множества - переполнение порядка; для большинства компьютеров вычисление на этом заканчивается;

2) число 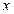по модулю меньше минимального по модулю ненулевого из чисел множества 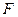- исчезновение порядка; это событие обычно не имеет таких катастрофических последствий, как переполнение, и многие компьютеры заменяют результат нулем без какого-либо указания на то, что это произошло. Однако есть вычисления, для которых такой факт важен;

3) число 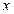совпадает с одним из чисел множества 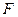- в этом случае 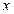представляется в ЭВМ точно;

4) число 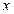находится в границах представления чисел данной системы 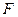, но не совпадает ни с одним из чисел 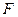- в этом случае оно приближается одним из чисел множества 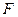по некоторому правилу, в результате возникает погрешность.

С точки зрения точности представления чисел в ЭВМ наибольший интерес представляет ситуация 4). В современных ЭВМ наиболее широко представлены два способа приближения чисел: округление и усечение.

Округление числа 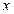- замена этого числа ближайшим к нему числом 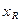из множества 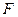; усечение включает в себя нормализацию числа 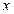и последующее отбрасывание лишних разрядов, в результате чего получается .

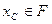Задание. Какой способ приближения является более точным, на сколько? Почему?