Синтез кодовой комбинации циклического кода

⇐ ПредыдущаяСтр 4 из 7Следующая ⇒

Кодовая комбинация циклического кода может быть получена двумя способами. Первый получается умножением информационной последовательности на образующий полином Р (х), что приводит к формированию неразделимого циклического кода. Неразделимость значительно усложняет процесс декодирования, поэтому на практике чаще используют второй способ, при котором информационная последовательность умножается на одночлен х^r и добавляется остаток от деления полученной последовательности на образующий полином. Это можно записать в виде формулы:

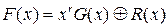(7)

где F (x) – кодовая комбинация циклического кода;

G (x) – информационная последовательность в полиномиальной форме;

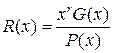- остаток от деления на образующий полином.

Для перевода двоичной последовательности в полиномиальную форму каждый бит (1 или 0) умножается на х в степени, соответствующей месторасположению этого бита.

Переведем последовательность, полученную в п. 1.1 в полиномиальную форму.

х ²³

х ²²

х ²¹

х ²⁰

х ¹⁹

х ¹⁸

х ¹⁷

х ¹⁶

х ¹⁵

х ¹⁴

х ¹³

х ¹²

х ¹¹

х ¹⁰

х ⁹

х ⁸

х ⁷

х ⁶

х ⁵

х ⁴

х ³

х ²

х ¹

х ⁰

Полученную кодовую комбинацию можно записать как:

G (x) = х ²³ + х ²² + х ¹⁶ + х ¹⁵ + х ¹³ + х ¹² + х ¹¹ + х ⁷ + х ⁵ + х ⁴ + х ³ + х ² + х + 1.

Умножим G (x) на одночлен х^r. Так как количество проверочных разрядов, рассчитанное в п. 1.2 равно семи, то умножаем на х ⁷

G (x) х ⁷ = х ³⁰ + х ²⁹ + х ²³ + х ²² + х ²⁰ + х ¹⁹ + х ¹⁸ + х ¹⁴ + х ¹² + х ¹¹ + х ¹⁰ + х ⁹ + х ⁸ + х ⁷.

Для получения разрешенной комбинации циклического кода разделим полученную последовательность на выбранный в п. 1.2 образующий полином. Процесс деления показан ниже.

Å	x ³⁰+ x ²⁹+ x ²³+ x ²²+ x ²⁰+ x ¹⁹+ x ¹⁸+ x ¹⁴+ x ¹²+ x ¹¹+ x ¹⁰+ x ⁹+ x ⁸+ x ⁷	x ⁷+ x ⁴+ x ³+1
x ³⁰+ x ²⁷+ x ²⁶+ x ²³		x ²³+ x ²²+ x ²⁰+ x ¹⁸+ x ¹⁷+ x ¹⁶+ x ¹⁵+ x ¹²+ x ¹¹+ x ¹⁰+ x ⁸+ x ⁷+ x ⁶+ x ⁵+ x ²+ x
Å	x ²⁹+ x ²⁷+ x ²⁶+ x ²²+ x ²⁰+ x ¹⁹+ x ¹⁸+ x ¹⁴+ x ¹²+ x ¹¹+ x ¹⁰+ x ⁹+ x ⁸+ x ⁷
x ²⁹+ x ²⁶+ x ²⁵+ x ²²
Å	x ²⁷+ x ²⁵+ x ²⁰+ x ¹⁹+ x ¹⁸+ x ¹⁴+ x ¹²+ x ¹¹+ x ¹⁰+ x ⁹+ x ⁸+ x ⁷
x ²⁷+ x ²⁴+ x ²³+ x ²⁰
Å	x ²⁵+ x ²⁴+ x ²³+ x ¹⁹+ x ¹⁸+ x ¹⁴+ x ¹²+ x ¹¹+ x ¹⁰+ x ⁹+ x ⁸+ x ⁷
x ²⁵+ x ²²+ x ²¹+ x ¹⁸
Å	x ²⁴+ x ²³+ x ²²+ x ²¹+ x ¹⁹+ x ¹⁴+ x ¹²+ x ¹¹+ x ¹⁰+ x ⁹+ x ⁸+ x ⁷
x ²⁴+ x ²¹+ x ²⁰+ x ¹⁷
Å	x ²³+ x ²²+ x ²⁰+ x ¹⁹+ x ¹⁷+ x ¹⁴+ x ¹²+ x ¹¹+ x ¹⁰+ x ⁹+ x ⁸+ x ⁷
x ²³+ x ²⁰+ x ¹⁹+ x ¹⁶
Å	x ²²+ x ¹⁷+ x ¹⁶+ x ¹⁴+ x ¹²+ x ¹¹+ x ¹⁰+ x ⁹+ x ⁸+ x ⁷
x ²²+ x ¹⁹+ x ¹⁸+ x ¹⁵
Å	x ¹⁹+ x ¹⁸+ x ¹⁷+ x ¹⁶+ x ¹⁵+ x ¹⁴+ x ¹²+ x ¹¹+ x ¹⁰+ x ⁹+ x ⁸+ x ⁷
x ¹⁹+ x ¹⁶+ x ¹⁵+ x ¹²
Å	x ¹⁸+ x ¹⁷+ x ¹⁴+ x ¹¹+ x ¹⁰+ x ⁹+ x ⁸+ x ⁷
x ¹⁸+ x ¹⁵+ x ¹⁴+ x ¹¹
Å	x ¹⁷+ x ¹⁵+ x ¹⁰+ x ⁹+ x ⁸+ x ⁷
x ¹⁷+ x ¹⁴+ x ¹³+ x ¹⁰
Å	x ¹⁵+ x ¹⁴+ x ¹³+ x ⁹+ x ⁸+ x ⁷
x ¹⁵+ x ¹²+ x ¹¹+ x ⁸
Å	x ¹⁴+ x ¹³+ x ¹²+ x ¹¹+ x ⁹+ x ⁷
x ¹⁴+ x ¹¹+ x ¹⁰+ x ⁷
Å	x ¹³+ x ¹²+ x ¹⁰+ x ⁹
x ¹³+ x ¹⁰+ x ⁹+ x ⁶
Å	x ¹²+ x ⁶
x ¹²+ x ⁹+ x ⁸+ x ⁵
Å	x ⁹+ x ⁸+ x ⁶+ x ⁵
x ⁹+ x ⁶+ x ⁵+ x ²
Å	x ⁸+ x ²
x ⁸+ x ⁵+ x ⁴+ x
	x ⁵+ x ⁴+ x ²+ x = R (x)

Итак, разрешенная комбинация циклического кода, в соответствии с формулой (7) имеет вид:

F (x)= х ³⁰ + х ²⁹ + х ²³ + х ²² + х ²⁰ + х ¹⁹ + х ¹⁸ + х ¹⁴ + х ¹² + х ¹¹ + х ¹⁰ + х ⁹ + х ⁸ + х ⁷ + x ⁵+ x ⁴+ x ²+ x.

Переведем ее в двоичный вид:

⇐ Предыдущая 1 2 345 6 7 Следующая ⇒

© 2023 :: MyLektsii.ru :: Мои Лекции
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав.
Копирование текстов разрешено только с указанием индексируемой ссылки на источник.