Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Для новых пользователей первый месяц бесплатно. Чат-бот для мастеров и специалистов, который упрощает ведение записей: — Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать; Начать пользоваться сервисом
Выбор образующего полинома циклического кода
|
|
Теоретические вопросы выбора оптимальных параметров и синтеза кодовых комбинаций циклического кода рассмотрены в [1, 2, 4].
Очевидно, что введение необходимой величины избыточности будет определяться длиной информационной части k, заданным значением допустимой вероятности ошибки Р но, кратностью обнаруживаемых ошибок t обни качеством самого канала связи.
Для инженерных расчетов широкое применение нашла модель потока ошибок, предложенная Л. П. Пуртовым, которая с достаточной для практики точностью описывает характеристики потока ошибок с пакетированием.
Исследуя статистику ошибок в канале связи, было замечено, что вероятность появления ошибок кратности t в n разрядной кодовой комбинации равна:
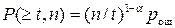; (1)
где α ‑ коэффициент группирования ошибок в дискретном канале.
Для канала без группирования (без памяти) α = 0, а при α = 1 ошибки сосредоточены в одном пакете.
Для обнаружения числа ошибок кратностью t необходим циклический код с кодовым расстоянием 
не менее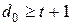 
тогда формула 1 примет вид:
. (2)
С некоторым приближением можно связать вероятность появления ошибок кратности t [ P (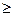
t, n)] с вероятностью необнаруженной УЗО ошибки P но и числом проверочных разрядов в кодовой комбинации следующим образом:
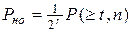(3)
Подставив в формулу 3 значение P (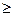 t, n) и, выполнив преобразование, вычислим r
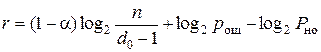(4)
При расчёте на ПК удобнее пользоваться десятичными логарифмами. После преобразований:
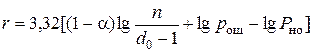(5)
Так как в этой формуле n = k + r, требуемое значение r может быть определено путем подбора величины r, удовлетворяющее неравенству:
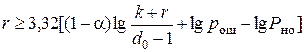. (6)
Подбор величины r необходимо начать с 3 и увеличивать на 1 до тех пор, пока не удовлетворится неравенство.
Зная величину r, т.е. величину высшей степени образующего полинома, следует выбрать соответствующий полином из таблицы 4.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Например, рассчитаем количество проверочных символов и выберем образующий полином для следующих исходных данных:
- вероятность ошибки в канале связи р ош = 3*10-5;
- вероятность необнаруженной ошибки декодером Р но = 1, 5*10-6;
- минимальное кодовое расстояние d = 3;
- коэффициент группирования α = 0, 6.
Подставим в формулу (6) исходные данные, а также значение r, начиная с 3:
r = 3: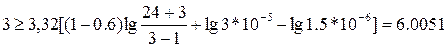 
- неравенство не выполняется
r = 4: 
- неравенство не выполняется
r = 5: 
- неравенство не выполняется
r = 6: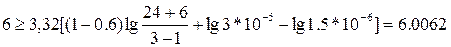 
- неравенство не выполняется
r = 7: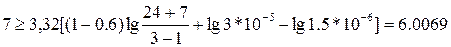 
- неравенство выполняется. Поэтому, значение r = 7.
Таблица 2.1
| Степень образующего полинома | Вид полинома |
| x +1 | |
| x 2+ x +1 | |
| x 3+ x +1 x 3+ x 2+1 | |
| x 4+ x +1 x 4+ x 3+1 x 4+ x 3+ x 2+ x +1 | |
| x 5+ x 3+1 x 5+ x 3+ x 2+1 x 5+ x 4+ x 2+ x +1 x 5+ x 4+ x 3+ x 2+1 | |
| x 7+ x 3+1 x 7+ x 4+ x 3+1 x 7+ x 3+ x 2+ x +1 | |
| x 8+ x 4+ x 3+ x +1 x 8+ x 5+ x 4+ x 3+1 x 8+ x 7+ x 5+ x +1 | |
| x 9+ x 4+ x 2+ x +1 x 9+ x 5+ x 3+ x 2+1 x 9+ x 6+ x 3+ x +1 | |
| x 10+ x 3+1 x 10+ x 4+ x 3+ x +1 x 10+ x 8+ x 3+ x 2+1 | |
| x 11+ x 2+1 x 11+ x 7+ x 3+ x 2+1 x 11+ x 8+ x 5+ x 2+1 | |
| x 12+ x 6+ x 4+ x +1 x 12+ x 9+ x 3+ x 2+1 x 12+ x 11+ x 6+ x 4+ x 2+ x +1 | |
| x 13+ x 4+ x 3+1 x 13+ x 10+ x 9+ x +1 x 13+ x 12+ x 11+ x 2+1 | |
| x 14+ x 13+ x 11+ x 9+1 x 14+ x 12+ x 10+ x 4+ x 2+ x +1 x 14+ x 12+ x 2+ x +1 | |
| x 15+ x 12+ x 3+ x +1 x 15+ x 13+ x 5+ x +1 x 15+ x 14+ x 13+ x 10+ x 2+ x +1 | |
| x 16+ x 15+ x 7+ x 2+1 x 16+ x 14+ x 12+ x 3+ x 2+ x +1 x 16+ x 12+ x 5+ x +1 |
Для выбора образующего полинома из таблицы 2.1 можно воспользоваться любым из трех приведенных полиномов для количества проверочных символов, равного 7. Выберем второй полином: x 7 + x 4 + x 3 + 1.
|
|