Марковская неоднородная цепь.

Допустим, что в системе S протекает Марковский дискретный процесс с дискретным временем. Пусть 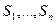- возможные состояния системы S и 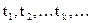- шаги, в которые система может перескакивать из состояния в состояние, то есть иметь Марковскую цепь.

Марковская цепь называется неоднородной, если переходные вероятности (хотя бы одна) зависят от номера шага k.

В этом случае переходные вероятности будем обозначать 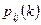. Тогда и матрица переходных вероятностей будет зависеть от k: 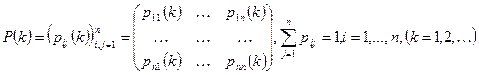, то есть матрица 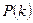при каждом 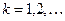является стохастической.

Для неоднородной Марковской цепи вектор-строка вероятностей состояний 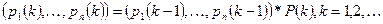(1)

Для неоднородной Марковской цепи имеет место следующая формула: (2)

У неоднородной Марковской цепи переходные вероятности 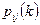(хотя бы одна из них) и, следовательно, матрица переходных вероятностей 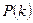зависят от номера k.

Вероятности состояний 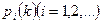неоднородной Марковской цепи на каждом шаге k вычисляется либо по реккурентной формуле (1), либо по формуле (2), где 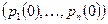- вектор начального распределения вероятностей состояний системы. [1]