Дискретный Марковский процесс с дискретным временем. Марковская однородная цепь.

Марковский случайный дискретный процесс, протекающий в системе S, характеризуется не только возможными состояниями, в которых система может пребывать случайным образом, но и теми моментами времени, в которые могут происходить ее переходы из состояния в состояние. Эти моменты времени могут быть заранее известны или случайны.

Случайный процесс, протекающий в системе, называется процессом с дискретным временем, если переходы системы из одного состояния могут осуществляться только в заранее определенные моменты времени 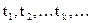называемые шагами этого процесса. В промежутках между соседними шагами система сохраняет свои состояния. Не исключается возможность, что на некоторых шагах система не изменит своего состояния.

Случайный процесс с дискретным временем можно представить случайной последовательностью (по индексу k) этих событий 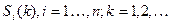которую называют также цепью.

Случайная последовательность называется Марковской цепью, если для каждого шага вероятность перехода из любого состояния 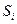в любое состояние 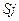не зависит от того, когда и как система 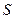оказалась в состоянии .

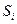Так как система 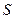в любой момент t может пребывать только в одном из состояний 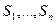, то при каждом k=1, 2, … события 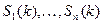несовместны и образуют полную группу.

Основными характеристиками Марковских цепей являются вероятности 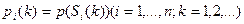событий .

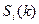Вероятности 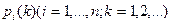называются вероятностями состояний.

Таким образом, вероятность i состояния на k шаге 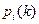есть вероятность того, что система S от k до (k+1) шага будет пребывать в состоянии 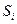. Сумма вероятностей этих событий для каждого 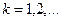равна 1: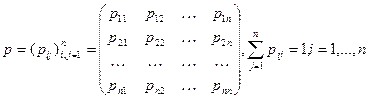 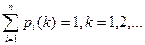. Если переходные вероятности не зависят от шагов k, то Марковская цепь называется однородной. Если же хотя бы одна вероятность изменяется с изменением шага k, то цепь называется неоднородной. Запишем переходные вероятности в виде квадратной матрицы n порядка, сумма элементов каждой строки равна 1.

Наличие на размеченном графе стрелок и соответствующих им переходных вероятностей из одного состояния в другое означает, что эти вероятности отличны от нуля. Напротив отсутствие стрелок из одного состояния в другое говорит о том, что соответствующие им переходные вероятности равны нулю. Вероятности задержек 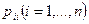можно подсчитать по формуле 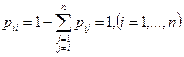. Вектор-строка вероятностей состояний 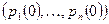в начальный момент времени t=0, непосредственно предшествующий первому шагу, называется вектором первоначального распределения вероятностей.

Для однородной Марковской цепи вектор-строка вероятностей состояний от k до (k+1) шага, равна произведению вектора-строки вероятностей состояний от (k-1) до k шага на матрицу переходных вероятностей: .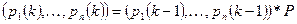

Для однородной Марковской цепи имеет место следующая формула: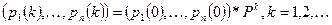

Дискретный случайный процесс с дискретным временем, протекающий в системе, характеризуется тем, что система может перескакивать из одного состояния в другое только в заранее определенные моменты времени, называемые шагами.

У однородной Марковской цепи переходные вероятности постоянны, не зависят от шагов (практически каждая переходная вероятность на любом шаге пренебрежимо мало отличается от постоянной для нее величины).

Основными вероятностными прогнозными характеристиками Марковской цепи являются вероятности состояний на любом шаге 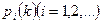.[1]

Все многообразие Марковских цепей подразделяется на эргодические и разложимые.

Разложимые Марковские цепи содержат невозвратные состояния, называемые поглощающими. Из поглощающего состояния нельзя перейти ни в какое другое. На графе поглощающему состоянию соответствует вершина, из которой не выходит ни одна дуга. В установившемся режиме поглощающему состоянию соответствует вероятность, равная 1.

Эргодические Марковские цепи описываются сильно связанным графом. Это означает, что в такой системе возможен переход из любого состояния 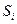в любое состояние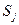 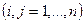за конечное число шагов.

Для эргодических цепей при достаточно большом времени функционирования (t стремится к бесконечности) наступает стационарный режим, при котором вероятности 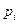состояний системы не зависят от времени и не зависят от распределения вероятностей в начальный момент времени, т.е. 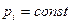.[4]