
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Порядок виконання роботи. 2.1. Використовуючи першу формулу Ерланга, визначити число каналів обслуговування, що забезпечать задану імовірність втрат Р( >0)
|
|
2.1. Використовуючи першу формулу Ерланга, визначити число каналів обслуговування, що забезпечать задану імовірність втрат Р (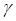 > 0), для трьох найпростіших потоків:
> 0), для трьох найпростіших потоків:
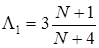 Ерл,
Ерл, 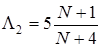 Ерл,
Ерл, 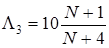 Ерл.
Ерл.
Значення Р(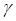 > 0) = N/ 1000, де N – номер по журналу
> 0) = N/ 1000, де N – номер по журналу
2.2. Привести таблицю і графіки залежностей Ev (L) (в одній системі координат):
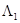
| 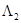
| 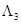
| |||
| v | Ev (L) | v | Ev (L) | v | Ev (L) |
| . | . | . |
2.3. Для всіх трьох випадків підрахувати пропускну здатність СМО з втратами.
Зробити висновки.
3. Контрольні питання.
3.1. Привести I формулу Ерланга.
3.2. Яка послідовність структурного синтезу СМО з явними втратами?
3.3. Як визначається пропускна здатність усієї СМО з явними втратами та її окремих каналів?
ЛАБОРАТОРНА РОБОТА №7
структурний синтез СМО з очікуванням
Мета: Вивчити другий розподіл Ерланга і характеристики якості систем з чергами та освоїти методи структурного синтезу СМО.
1. Теоретичні відомості
1.1 Другий розподіл Ерланга
v- канальна СМО обслуговує найпростіший потік викликів. Час обслуговування одного виклику - випадкова величина, розподілена за експоненціальним законом з параметром прийнятим за одиницю часу (h= 1у.о.ч.). Параметр потоку виклику L, можна розглядати як інтенсивність навантаження, що надходить. При зайнятості всіх v виходів виклик, що надійшов, стає в чергу й обслуговується після деякого чекання. Загальне число викликів, що знаходяться в системі на обслуговуванні та в черзі, позначимо 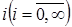 та назвемо станом системи. При
та назвемо станом системи. При 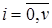 величина i характеризує число зайнятих виходів у системі, при
величина i характеризує число зайнятих виходів у системі, при 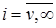 число зайнятих виходів дорівнює v, а різниця
число зайнятих виходів дорівнює v, а різниця  є довжина черги. Параметр потоку звільнень визначається числом зайнятих виходів і в першому випадку, при
є довжина черги. Параметр потоку звільнень визначається числом зайнятих виходів і в першому випадку, при 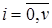 , залежить від стану системи i, а у другому, при
, залежить від стану системи i, а у другому, при 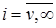 , має постійне значення v.
, має постійне значення v.
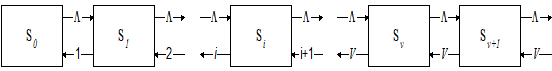
Рисунок 7.1. Граф станів СМО з чеканням
Зазначимо, що при інтенсивності навантаження, що надходить L, рівній або більшій числа каналів системи v, з імовірністю 1 будуть постійно зайняті усі канали і черга буде необмежено зростати. Тому, щоб система могла функціонувати нормально и черга не росла безмежно, необхідно дотримуватися умови 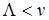 .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Імовірність того, що система в сталому режимі знаходиться в стані i (Pi.) визначаємо згідно другого розподілу Ерланга:
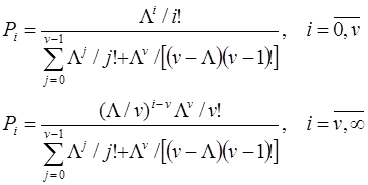 (7.1)
(7.1)
1.2 Характеристики якості систем M/M/V/W
До основних характеристик якості систем M/M/V/W відносять:
- Імовірність чекання для виклику, що надійшов.
Для найпростішого потоку викликів вона співпадає з імовірністю зайнятості усіх виходів у системі, тобто з імовірністю втрат за часом:
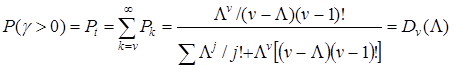 (7.2)
(7.2)
Вираз (7.2) називається другою формулою Ерланга.
Слід зазначити, що завжди 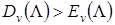 , тобто при однаковій інтенсивності поступального навантаження імовірність чекання в системі з чеканням вище, ніж імовірність втрати виклику в системі з явними втратами Зазначене перевищення втрат пояснюється тим, що при звільненні виходу в системі з явними втратами він дається виклику, що надходить, а в системі з очікуванням при наявності черги - що очікує. Виклик, що знову надійшов, у цьому випадку, вимушений ставати в чергу.
, тобто при однаковій інтенсивності поступального навантаження імовірність чекання в системі з чеканням вище, ніж імовірність втрати виклику в системі з явними втратами Зазначене перевищення втрат пояснюється тим, що при звільненні виходу в системі з явними втратами він дається виклику, що надходить, а в системі з очікуванням при наявності черги - що очікує. Виклик, що знову надійшов, у цьому випадку, вимушений ставати в чергу.
- Інтенсивність обслугованого навантаження.
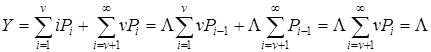 (7.3)
(7.3)
Через відсутність явних втрат повідомлень інтенсивність навантаження, що надходить, збігається з інтенсивністю обслугованого навантаження і надлишкове навантаження відсутнє. Оскільки для найпростішого потоку інтенсивність потенційного навантаження дорівнює інтенсивності навантаження, що надходить, втрачене навантаження також відсутнє. Проте не завжди в системі з очікуванням втрати по навантаженню дорівнюють нулю. При обслуговуванні примітивного потоку (така модель тут не розглядається) джерело, за рахунок очікування в середньому менше знаходиться у вільному стані, чим у системі без втрат. Це призводить до зниження інтенсивності потоку викликів і навантаження, що надходить, стає менше потенційного навантаження. І хоча усі виклики, що надходять, обслуговуються (рівність (7.3) вірна), втрати по навантаженню мають місце.
- Імовірність перевищення довжини черги заданої величинип.
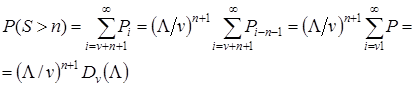 (7.4)
(7.4)
- Середня довжина черги.
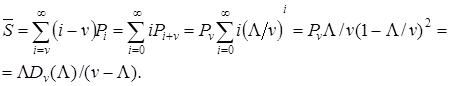 (7.5)
(7.5)
Величина 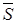 є інтенсивність навантаження, утворюваної викликами, що очікують, а
є інтенсивність навантаження, утворюваної викликами, що очікують, а 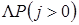 - інтенсивність потоку затриманих викликів, де кожний затриманий виклик у середньому очікує
- інтенсивність потоку затриманих викликів, де кожний затриманий виклик у середньому очікує  . Тоді
. Тоді
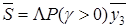 . (7.6)
. (7.6)
- Середня тривалість очікування.
Для затриманого виклику:
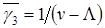 , (7.7)
, (7.7)
для будь-якого виклику, що надійшов:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
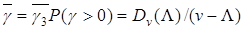 (7.8)
(7.8)
Величини 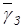 та
та 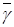 виражені в умовних одиницях часу.
виражені в умовних одиницях часу.
|
|
