Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Моделювання процесу обслуговування в СМО.

Функція розподілу проміжку між викликами , а функція розподілу тривалості обслуговування . Програма моделювання має містити два генератора випадкових величин z и x із заданими функціями A (t) и B (t), змінні t_o збереження моменту надходження чергового виклику та t₁, t₂,..., t_v для збереження моменту звільнення i -го () каналу.

Для спрощення пояснень приймемо v = 3 и проаналізуємо роботу алгоритму з моменту надходження п’ятого виклику. Перший генератор формує чергове випадкове число z ₅, що відповідає надходженню п’ятого виклику . Припустимо, що до моменту перший канал був зайнятий четвертим викликом, а другий і третій, відповідно другим і третім. Тоді: , , 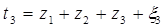. Кожне з чисел t₁ , t₂,, t₃ визначає момент звільнення відповідного каналу.

При послідовному занятті каналів значення t_o почергово порівнюється з t₁, t₂,, t_v, поки не знаходиться комірка з моментом звільнення 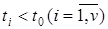. Припустимо, що и , а . Це означає, що до моменту надходження п’ятого виклику перший і другий канал були зайняті, а третій вже звільнився і може прийняти на обслуговування п’ятий виклик. Тоді t₃ присвоюється t₀, потім генерується випадкове число x ₅, що визначає тривалість обслуговування п’ятого виклику. Доданням числа x ₅ до t₃ п’ятий цикл закінчується.

Шостий цикл починається з генерації випадкового числа z₆. Як раніше, t₀=t₀+z₆. Потім здійснюється почергове порівняння вмісту нульової комірки з вмістом решти комірок. Якщо тепер виявиться, що , і 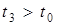, то шостий виклик буде втрачений і на цьому цикл закінчиться.

Для підрахунку числа надійшедших К_вик і втрачених К_вт. викликів використовують два лічильники. В перший додається одиниця при кожній генерації числа z, а в другий - при кожній втраті виклику. Відношення К_вик/К_вт. дає по закінченні чергової серії статистичну оцінку втрат викликів.

2. Порядок виконання роботи:

2.1. Початкові умови моделювання:

a) Параметр потоку: (викл./хв), де N - номер за журналом.

b) Середній час обслуговування h і число каналів v:

c) На початку моделювання в системі зайнято два канали.

2.2. Порядок моделювання.

a) Моделювання здійснювати на інтервалі: [ t ₁, t ₂]хв.

t ₁ =N+ 1, t ₂ =N+ 200, де N - номер за журналом.

b) Надходження виклику моделюється аналогічно лабораторній роботі №1, запам’ятовується в змінній t_над і підраховується лічильником К_вик.

c) Процес обслуговування моделюється за експоненціальним законом розподілу.

; .

d) Час звільнення каналу визначається: t_зв.i = t_над.i + x_i;

e) Канали займаються послідовно. Якщо до моменту надходження виклику зайняті всі канали, то він втрачається і підраховується кількість втрачених викликів К_вт.

Результати моделювання зводяться в таблицю:

r	z		tнад	tзв	N каналу
r 1	-	x 1	-	t0 + x 1
r 2	-	x 2	-	t0 + x 2
r 3	z 3	x 3	tнад. 3	tнад. 3 + x 3	Втрата

2.3. Визначити модельну імовірність втрати виклику:

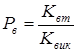
К_вт - кількість втрачених викликів;

К_вик - загальна кількість викликів

2.4. Визначити Р_в за I формулою Ерланга: ,

де .

Зробити висновки.

3. Контрольні питання.

3.1. Визначення та практичне вимірювання характеристик якості систем з втратами:

- імовірність втрати виклику;

- імовірність втрати за часом;

- імовірність втрати за навантаженням.

3.2. Використання символіки Кендала-Башаріна.

3.3. Побудувати граф станів системи, що моделювалась. Визначити типи потоків.

ЛАБОРАТОРНА РоБОТА №5

Аналіз V -канальної СМО з явними втратами

Мета: Дослідити 1-й розподіл Ерланга і характеристики якості СМО з явними втратами.

1. Теоретичні відомості

1.1. Перший розподіл Ерланга.

На вхід v -канальної СМО з явними втратами надходить найпростіший потік викликів з параметром l викл/хв., тривалість обслуговування виклику – випадкова величина, розподілена за експоненціальним законом з середнім значенням, прийнятим зо 1 у.о.ч. Тоді параметр потоку, виражений в Ерл можна вважати інтенсивністю навантаження, що надходить L. Тобто маємо систему М/М/v/L. Граф станів такої системи наведено на рис. 5.1.

Рисунок 5.1. Граф станів СМО М/М/v/L

Імовірності усіх станів системи (в усталеному режимі) дає перший розподіл Ерланга:

(5.1)

Перший розподіл Ерланга має максимуми залежно від співвідношення між L і v. Якщо L > v, перший розподіл Ерланга має 1 максимум i = v. Якщо L £ v і L - дробове число, перший розподіл Ерланга має також 1 максимум i = [ L ]. Якщо ж L £ v і L - ціле число, перший розподіл Ерланга має 2 максимуми: i = L та i = L – 1.

1.2. Характеристики якості СМО з явними втратами

До основних характеристикам якості обслуговування такої СМО відносять:

- Імовірність втрат за часом

(5.2)

Формулу (5.2) звичайно називають першою формулою Ерланга.

- Імовірність втрати виклику

Для найпростішого потоку викликів:

(5.3)

Тобто, імовірність втрати виклику співпадає з імовірністю втрат за часом.

- Інтенсивність обслугованого навантаження

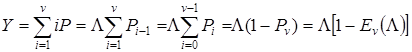(5.4)

- Інтенсивність потенціального навантаження

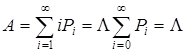(5.5)

Рівність інтенсивностей потенціального навантаження і навантаження, що надходить зумовлює рівність інтенсивностей втраченого L_вт та надлишкового R навантаження:

(5.6)

З (5.6) безпосередньо витікає рівність втрат по навантаженню і по виклику. Таким чином, усі три види втрат рівні між собою. Пояснюється це двома властивостями найпростішого потоку: стаціонарністю і відсутністю післядії.

– Пропускна здатність 1 каналу

Пропускна здатність 1 каналу системи з явними втратами залежить від способу зайняття каналу – випадкового чи послідовного.

Для випадкового способу зайняття каналу (система M/M/V/L//R) кожний з V каналів системи має однакову пропускну здатність:

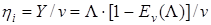(5.7)

Для послідовного способу зайняття каналу (система M/M/V/L//S) пропускна здатність i -го каналу визначається:

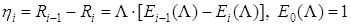(5.8)