
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
в гладкой цилиндрической трубе
|
|
Полагая суммарное касательное напряжение в потоке постоянной величиной и принимая гипотезу Прандтля для турбулентных напряжений, запишем (5.38) в виде
 . (5.43)
. (5.43)
По мере приближения к стенке турбулентные пульсации затухают, напряжение τ Т уменьшается и в непосредственной близости от стенки становится столь малым по сравнению с τ μ , что в пределах пристеночного слоя можно принять τ 0 =τ μ .
По мере удаления от стенки роль турбулентных пульсаций возрастает и, начиная с некоторого расстояния, значение τ T многократно превосходит значение напряжения τ μ , так что для этой области потока можно принять τ 0 =τ T.
Для пристеночной области потока (ламинарного подслоя),
 , (5.44)
, (5.44)
где τ μ =const - напряжение трения на стенке трубы. Отсюда

Интегрируя это уравнение, получим

При y= 0, U= 0 постоянная интегрирования С =0. Таким образом, в ламинарном подслое распределение скорости носит линейный характер:
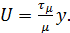 (5.45)
(5.45)
В области турбулентного течения
 . (5.46)
. (5.46)
Используя для длины пути перемешивания формулу Прандтля l=ϰ y, получим
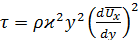 , (5.47)
, (5.47)
откуда
 . (5.48)
. (5.48)
Обозначая  и интегрируя уравнение (5.48), находим
и интегрируя уравнение (5.48), находим
 (5.49)
(5.49)
Для определения постоянной С используем условие на границе между турбулентным ядром потока и ламинарным подслоем:  ;
;  . Здесь δ л – толщина ламинарного подслоя, а Uл – скорость на его границе.
. Здесь δ л – толщина ламинарного подслоя, а Uл – скорость на его границе.
Записывая уравнение (5.49) для границы ламинарного подслоя, получим
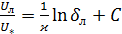 .
.
Отсюда
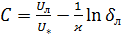 . (5.50)
. (5.50)
Исходя из уравнения (5.45) для границы ламинарного подслоя, напишем
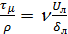 , так как
, так как 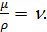
С учетом скорости U* выражение для τ μ / ρ можно представить в виде
 или
или 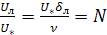 , (5.51)
, (5.51)
где N - безразмерный комплекс, аналогичный по структуре числу Рейнольдса.
Из (5.51) толщина ламинарного подслоя
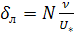 . (5.52)
. (5.52)
Подставляя выражения (5.51 и (5.52) в (5.50), получим
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
 , (5.53)
, (5.53)
а подставляя (5.53) в (5.49), имеем
 , или
, или 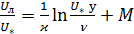 ,
,
где 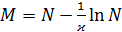 .
.
Величины 1/ϰ и 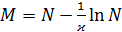 можно определить опытным путем.
можно определить опытным путем.
Так, из опытов И. И. Никурадзе получена формула, выражающая универсальный логарифмический закон распределения скоростей в гладких трубах:
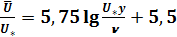 . (5.54)
. (5.54)
Положив в (5.54) y=r 0, определим скорость на оси трубы 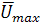 :
:
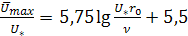 . (5.55)
. (5.55)
Зная закон распределения скоростей, можно найти величину коэффициента гидравлического трения. Для гидравлически гладких труб, исходя из формулы (5.54), можно записать для средней скорости потока
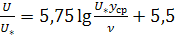 , (5.56)
, (5.56)
где yср = 0, 223 U * - расстояние от стенки до слоя, скорость в котором равна средней скорости U.
Ранее была получена зависимость
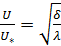 ,
,
подставляя которую в (5.56), получим известную формулу Прандтля для коэффициента гидравлического трения в гладких трубах:
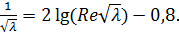 (5.57)
(5.57)
Недостаток формулы (5.57) в том, что связь λ и числа Re выражена в неявной форме. Этого недостатка нет, например, у эмпирической формулы Конакова
 . (5.58)
. (5.58)
Наряду с логарифмическими формулами существуют степенные. Например, широко применяется эмпирическая формула Блазиуса, пригодная при Re< 100000:
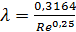 . (5.59)
. (5.59)
Этой формуле отвечает степенное выражение для распределения скорости потока по сечению трубы (применение которой ограничено тем же условием):
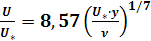 , (5.60)
, (5.60)
где у - расстояние от стенки трубы.
Это уравнение известно под названием закона Блазиуса.
Для максимальной скорости на оси трубы (y=r 0)
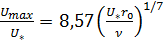 . (5.61)
. (5.61)
Из равенств (5.60) и (5.61) получим
 .
.
Литература по содержанию лекции:
1. Чугаев Р. Р. Гидравлика (Техническая механика жидкости). - Л.: Энергоиздат, 1982. - 672 с.
2. Штеренлихт Д. В. Гидравлика. - М.: Энергоатомиздат, 1985. - 640 с.
|
|
