Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Уравнения Рейнольдса

Подставив в уравнения Навье-Стокса (4.29) вместо компонент скорости их выражения (5.34) через осредненные и пульсационные скорости, можно получить уравнения Рейнольдса для установившегося (в среднем) турбулентного движения:

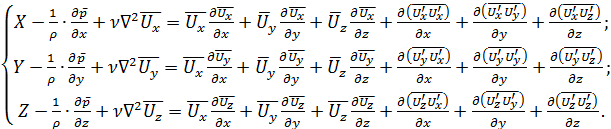(5.37)

В отличие от уравнений Навье-Стокса каждое из уравнений (5.37) включает три дополнительных члена, зависящих от пульсаций скорости. Представив каждый из этих членов в форме 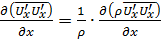, перенесём в уравнениях Рейнольдса члены, зависящие от пульсаций, в левую часть. Ограничимся первым уравнением:

.

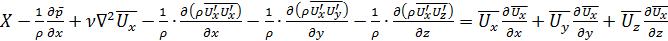Наряду с членами, выражающими действие вязкостных напряжений,

,

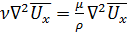уравнения Рейнольдса содержат члены, выражающие действие осреднённых турбулентных касательных напряжений 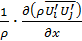, где 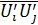- осреднённое произведение пульсационных скоросте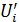й и 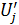(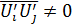, так как 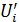и 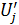зависимы друг от друга).

Полные касательные напряжения - сумма вязкостных и турбулентных:

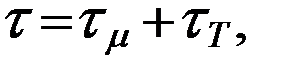(5.38)

причем турбулентные касательные напряжения обладают свойством взаимности (τ _ij=τ _ji) и выражаются как

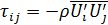. (А)

Выражение (А) получил О. Рейнольдс (в 1895 г.).