
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнения движения вязкой жидкости (Навье-Стокса)
|
|
Дифференциальные уравнения движения вязкой жидкости можно составить, дополнив уравнения Эйлера (4.2) слагаемыми, учитывающими вязкость жидкости:
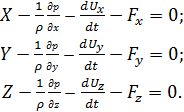 (4.3)
(4.3)
где Fx, Fy, и Fz - проекции сил вязкости, отнесенные к единице массы жидкости.
Определим силы Fx, Fy и Fz, полагая, что жидкость движется слоями, без перемешивания. Силы вязкости вызывают касательные и нормальные напряжения.
Выделим элемент жидкости в форме параллелепипеда с ребрами dx, dy, dz и определим проекции сил вязкости, действующих на те грани параллелепипеда, которые образуют трехгранный угол с вершиной А (рис. 4.2). Введем двойную индексацию напряжений. Первый индекс указывает на то, что площадка, для которой определяется напряжение, расположена нормально к соответствующей оси координат, а второй индекс - направление действия напряжения. Тогда проекции сил:
на ось 0x pxxdydz; τ yxdxdz; τ zxdxdy;
на ось 0y pyydxdz; τ xydydz; τ zydxdy;
на ось 0z pzzdxdy; τ xzdydz; τ yzdxdz.
Проекции сил, действующих на грани трехгранного угла с вершиной С':
ось 0x 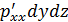 ;
; 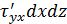 ;
; 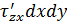 ;
;
ось 0y 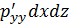 ;
; 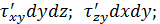
ось 0z 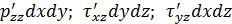 .
.
Здесь для оси 0x: 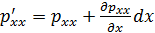 ;
; 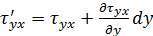 ;
; 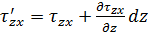 .
.
Определим сумму проекций сил вязкости на ось 0x. Учитывая, что силы, действующие на грани угла с вершиной C ′, направлены противоположно силам, действующим на грани угла с вершиной А, получим
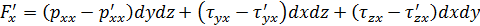 .
.
Но
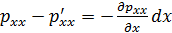 ;
; 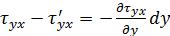 ;
; 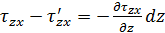 .
.
Поэтому, делая соответствующую подстановку, найдем
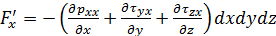 .
.
Сила Fx, входящая в уравнение (4.3), - это проекция силы вязкости, отнесенной к единице массы жидкости, то есть 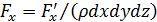 , поэтому
, поэтому
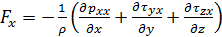 . (4.4)
. (4.4)
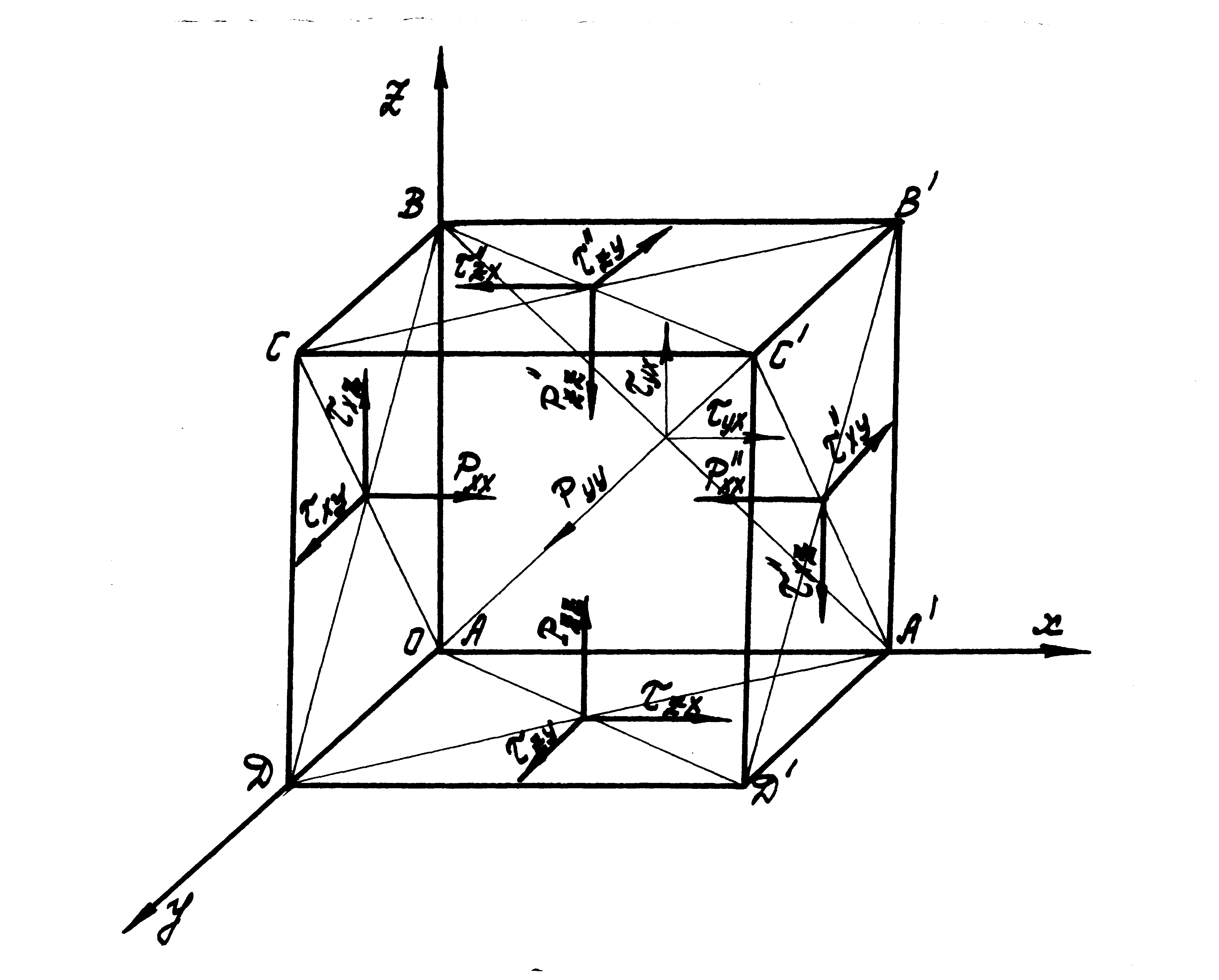 Рис. 4.2
Рис. 4.2
|
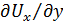 . Поэтому, согласно закону трения Ньютона:
. Поэтому, согласно закону трения Ньютона:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
τ yx=µ∂ Ux / ∂ y,
и, аналогично, на нижней грани dxdy:
τ zx=µ∂ Ux / ∂ z.
Рассмотрим производную ∂ pxx / ∂ x. Здесь pxx - нормальное к площадке dydz напряжение, обусловленное влиянием вязкости (сжатие в условиях торможения и растяжение при ускоренном движении). Поэтому можно допустить, что напряжение pxx также определяется по закону Ньютона:
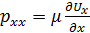 .
.
Тогда
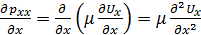 .
.
Рассуждая аналогично и делая соответствующие подстановки в уравнение (4.4), получим
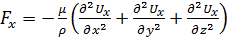 или, так как µ/ρ =ν,
или, так как µ/ρ =ν, 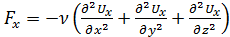 .
.
Аналогично для проекций сил вязкости на оси 0y и 0z:
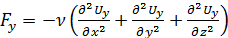 ;
; 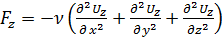 .
.
Вводя выражения для сил Fx, Fy, Fz в (4.3), получим дифференциальные уравнения движения вязкой жидкости - уравнения Навье-Стокса:
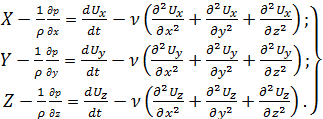 . (4.5)
. (4.5)
Более кратко уравнения Навье-Стокса записываются с помощью дифференциального оператора Лапласа 2-го порядка 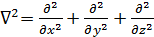 :
:
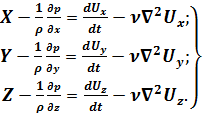 . (4.6)
. (4.6)
При решении задач движения несжимаемой жидкости к уравнениям (4.6) необходимо добавить уравнение неразрывности (3.17)
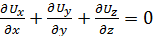 ,
,
чтобы получить замкнутую систему из четырех уравнений для определения четырех неизвестных функций Ux, Uy, Uz, p.
Кроме того, для определения произвольных постоянных и функций, появляющихся при интегрировании, должны быть сформулированы так называемые краевые условия, то есть совокупность начальных и граничных условий.
Начальные условия (в случае нестационарного движения) указываются заданием поля скоростей и давлений в некоторый начальный момент времени.
Граничные условия для случая вязкой жидкости состоят в признании того, что частицы жидкости, непосредственно соприкасающиеся с поверхностью твердого тела, прилипают к ней и поэтому имеют одинаковую с ней скорость.
В частном случае при обтекании неподвижного тела граничное условие для скорости жидкости должно быть записано в виде U = 0.
Уравнения (4.5) движения реальной (вязкой) жидкости - это нелинейные уравнения второй степени в частных производных. В общем виде эти уравнения не интегрируются. Их решение возможно лишь для частных случаев, допускающих упрощения путем отбрасывания тех или иных членов.
|
|
