
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретическая чать
|
|
ЛАБОРАТОРНАЯ РАБОТА №7
Тема: ПОСТРОЕНИЕ ДИАГРАММ
Цель работы: Научиться строить диаграммы разного уровня сложности.
@ Задание (в соответствии с индивидуальным вариантом)
1. Изучить теоретические вопросы по теме лабораторной работы.
2. Построить графики функций f(x).
3. Отчет представить в тетради (расчет области допустимых значений (ОДЗ)) и в электронном виде.
4. Лист книги Excel должен содержать:
a. написанную в редакторе формул функцию, по которой строится график,
b. таблицу значений функции,
c. график функции (название графика, подписи осей).
5. Диапазон изменений переменной Х и шаг ее изменения подберите самостоятельно.
Теоретическая чать
Пример 1
Построить график функции  (рис.1).
(рис.1).
Решение
При построении графика следует обратить внимание на область определения функции. В данном случае функция не существует при обращении знаменателя в ноль. Решим уравнение: 4 x + 8 ≠ 0; 4 x ≠ − 8; x ≠ − 2. Следовательно, при определении значений аргумента следует помнить, что при x = − 2 функция не определена. На рис.5.8 видно, что значение аргумента задано в два этапа, не включая (-2) с шагом 0, 2.
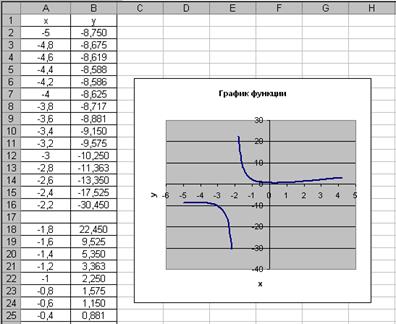
Рис. 1. График функции 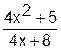
Пример 2
Построить график функции 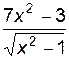 (рис.2).
(рис.2).
Решение
ОДЗ: x2− 1≥ 0 Þ x2 ≥ 1 Þ x=±1 Þ x Î (− ¥; − 1)È (1; +¥). Определение значения аргумента следует провести в два этапа. Например, от -5 до -1, а затем от 1 до 5, с шагом 0, 5.
Пример 3
Построить график функции 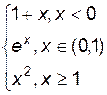 (рис.3).
(рис.3).
Решение
При построении этого графика следует использовать функцию ЕСЛИ(). Например, в ячейке А7 (рис.3) находится начальное значение аргумента, тогда в ячейку В7 необходимо ввести формулу: =ЕСЛИ(A7< 0; 1+A7; ЕСЛИ(A7> =1; A7^2; EXP(A7))).
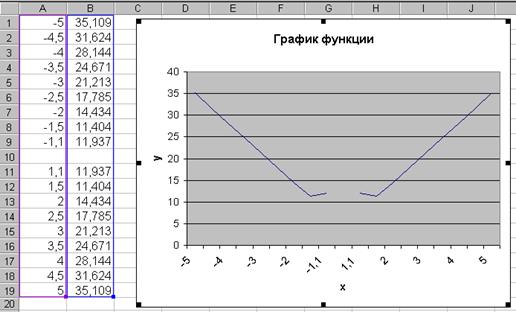
Рис. 2. График функции 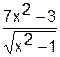
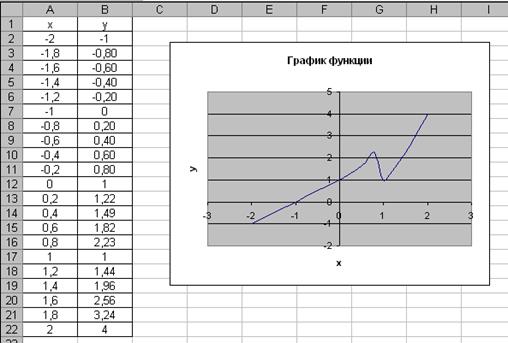
Рис. 3. График функции 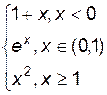
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Пример 4
Изобразите линию, заданную неявно уравнением: 4y2 +5x2 –20=0.
Решение
Заметим, что заданная уравнением f(x, y)=0функция описывает кривую линию под названием эллипс. Это можно доказать, если произвести элементарные математические операции:
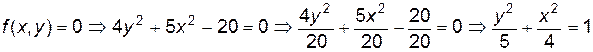 .
.
В связи с тем, что линия задана неявно, для ее построения необходимо разрешить заданное уравнение относительно переменной У:
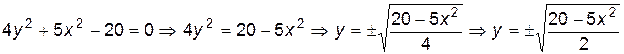 .
.
После проведенных преобразований можно увидеть, что линию f(x, y)можно изобразить, построив графики двух функций: 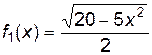 и
и 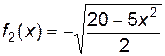 в одной графической области.
в одной графической области.
Перед построением определим ОДЗ функций f1(x) и f2(x). Поскольку эти функции содержат в числителе выражение под знаком квадратного корня, то обязательным условием их существования будет выполнение следующего неравенства:
20 − 5 x2 ≥ 0 Þ − 5 x2 ≥ − 20 Þ x2 ≤ 4 Þ x ≤ ±2 Þ − 2 ≤ x ≤ 2 Þ xÎ [− 2, 2].
Теперь перейдем к построению графика. Для этого в диапазон А2: А42 введем значения аргумента (от -2 до 2 с шагом 0, 1). В ячейку В2 введем формулу для вычисления значений функции f1(x):
=КОРЕНЬ(20-5*$A3^2)/2,
а в С2 для вычисления f2(x):
=-КОРЕНЬ(20-5*$A3^2)/2.
Далее скопируем эти формулы до В42 и С42 соответственно (рис.4). Затем выделим диапазон А2: С42 и, воспользовавшись Мастером диаграмм, построим графики функций f1(x) и f2(x) в одной графической области.
Затем выделим диапазон А2: С42 и, воспользовавшись Мастером диаграмм, построим графики функций f1(x) и f2(x) в одной графической области (рис. 5).

Рис. 4. Создание таблицы в ячейках A2: C42
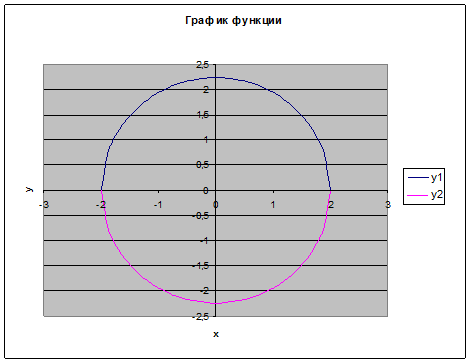
Рис.5. График функции 4y2 +5x2 –20=0
Пример 5
Изобразите линию, заданную неявно: 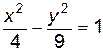 .
.
Решение
Уравнение описывает линию под названием гипербола. Разрешим его относительно переменной У:
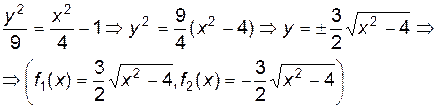 .
.
Найдем ОДЗ функций f1(x) и f2(x): x2 − 4 ≥ 0 Þ x Î (− ¥, − 2] и[2, +¥).
Проведенные исследования показывают, что для построения графика необходимо значения аргумента задавать в два этапа, так как в диапазоне от -2 до 2 функция неопределенна. Задание значений функций f1(x) и f2(x) и построение графика выполняется аналогично ранее рассмотренным примерам. Результаты представлены на рис. 6 и 7.

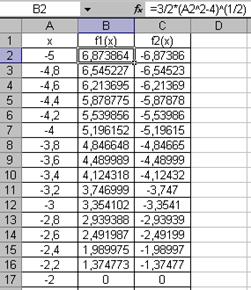
Рис. 6. Создание таблицы в ячейках А2: С52
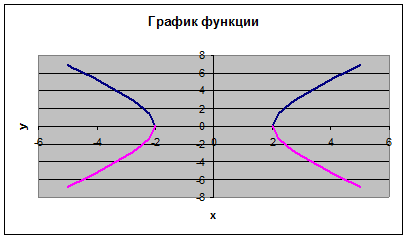
Рис. 7. График функции 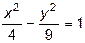
Варианты заданий
1. Построить график функции f(x).
| № | f(x) | № | f(x) | № | f(x) | |
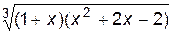
| 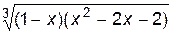
| 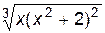
| ||||
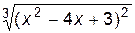
| 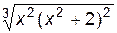
| 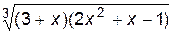
| ||||
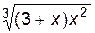
| 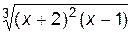
| 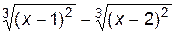
| ||||
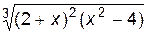
| 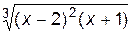
| 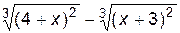
| ||||
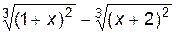
| 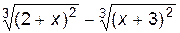
| 
| ||||
| 
| 
| ||||
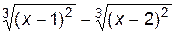
| 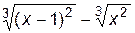
| 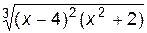
| ||||
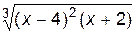
| 
| 
| ||||
| 
| 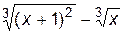
| ||||
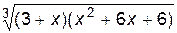
| 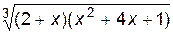
| 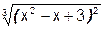
| ||||
2. Построить график функции f(x).
| № | f(x) | № | f(x) | № | f(x) |
| 
| 
| |||
| 
| 
| |||
| 
| 
| |||
| 
| 
| |||
| 
| 
| |||
| 
| 
| |||
| 
| 
| |||
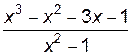
| 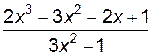
| 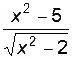
| |||
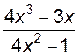
| 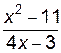
| 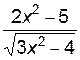
| |||
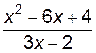
| 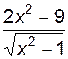
| 
|
3. Построить график функции f(x).
| f(x) | № | f(x) | № | f(x) | |
| 
| 
| |||
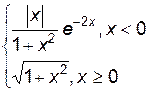
| 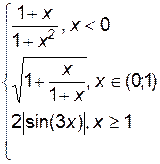
| 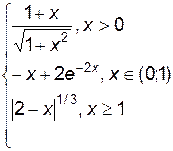
| |||
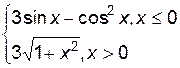
| 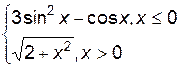
| 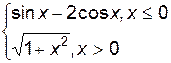
| |||
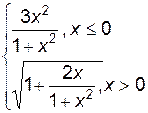
| 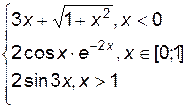
| 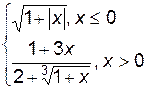
| |||
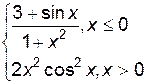
| 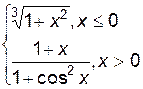
| 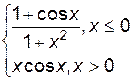
| |||
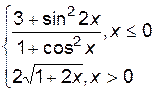
| 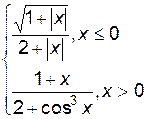
| 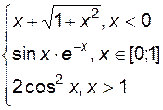
| |||
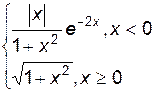
| 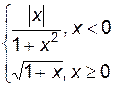
| 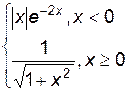
| |||
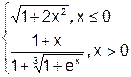
| 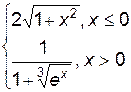
| 
| |||
| 
| 
| |||
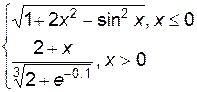
| 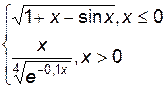
| 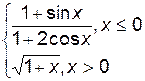
|
4. Изобразите линии заданные неявно уравнением f(x, y)=0
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
| № | f(x) | № | f(x) | № | f(x) |
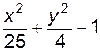
| 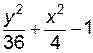
| 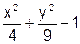
| |||
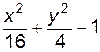
| 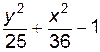
| 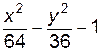
| |||
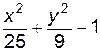
| 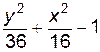
| 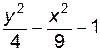
| |||
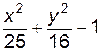
| 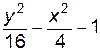
| 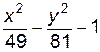
| |||
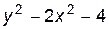
| 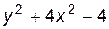
| 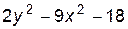
| |||
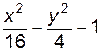
| 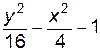
| 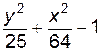
| |||
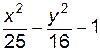
| 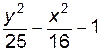
| 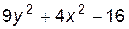
| |||
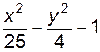
| 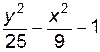
| 
| |||
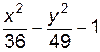
| 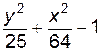
| 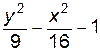
| |||
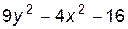
| 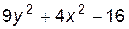
| 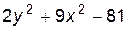
|
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Как построить диаграмму в Excel 2003?
2. Как построить диаграмму в Excel 2007?
3. Какие типы диаграмм можно построить в Excel?
4. Как можно вызвать Мастер диаграмм (Excel 2003)?
a. За сколько шагов можно построить диаграмму с помощью Мастера диаграмм (Excel 2003)?
b. На каком шаге задается диапазон ячеек для построения диаграммы?
c. На каком шаге задается название диаграммы?
5. Что такое легенда в диаграммах?
6. Как выполнить форматирование диаграммы?
|
|
