
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекция 4. Понятие энергетического спектра
|
|
Понятие энергетического спектра
Следует обратить внимание, что в ряд Фурье раскладываются функции с бесконечной энергией, но конечной мощности, т.е. энергией в единицу времени
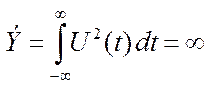 (15)
(15)
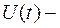 сигнал
сигнал
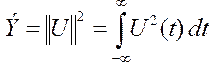
(16)
Квадрат нормы носит понятие энергии сигнала.
Мощность конечная
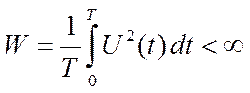 (17)
(17)
Энергия сигнала – сумма всех компонент из которых складывается обобщённый ряд Фурье (т.е. сигнал, разложенный в ряд по ортонормированной базисной системе).
Если сигнал импульсный, то у него энергия конечная 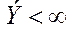 , а мощность равна 0.
, а мощность равна 0.
Почему? Импульсные сигналы не имеют периода. Амплитудные коэффициенты при разложении последовательности импульсов в комплексный ряд Фурье, станут неограниченно малыми при переходе к одиночному импульсу, т.е. при 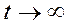 .
.
Фурье-преобразование некоторых функций
1)  1
1
t
0 Т
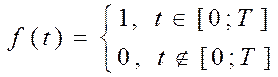
 |
амплитудный спектр,
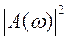 - энергетический спектр
- энергетический спектр
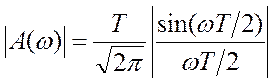
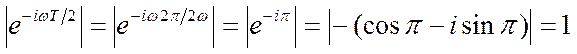
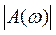
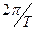
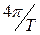
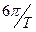
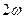
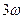
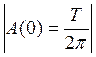 – физический смысл – площадь под кривой (делённая на
– физический смысл – площадь под кривой (делённая на 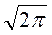 )
)
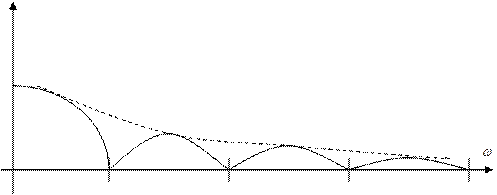
Огибающая спектра

спадает медленно – разрыв функции
Ширина спектра 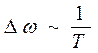
2)
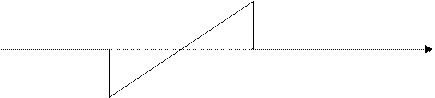
t
0 Т/2
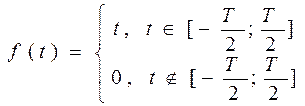
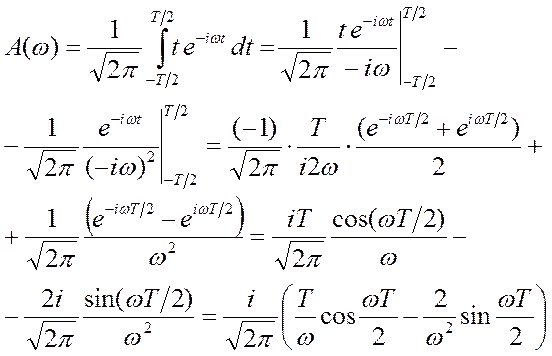
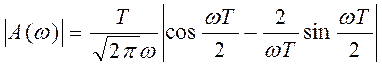
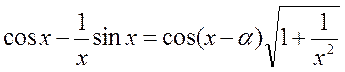
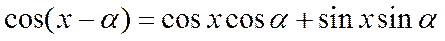
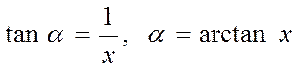
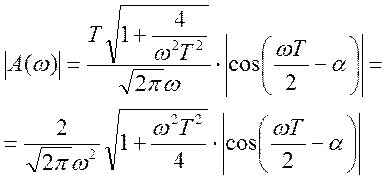
Вынесем 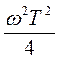 за корень, где
за корень, где 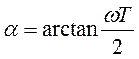
Проверим:
а) 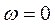
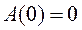 – действительно, площадь под кривой равна нулю
– действительно, площадь под кривой равна нулю
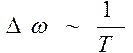 б)
б) 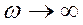
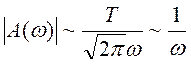 – разрыв функции
– разрыв функции
в) ширина спектра
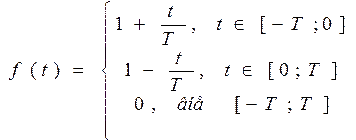
3)

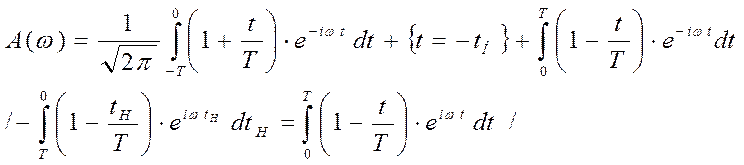
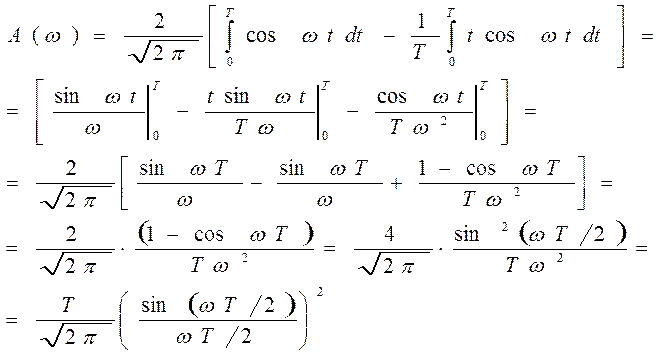
Проверяем:
а) 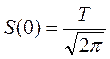 действительно площадь под кривой Ѕ (2Т х 1)
действительно площадь под кривой Ѕ (2Т х 1)
б) огибающая 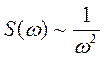 разрыв производной
разрыв производной
в) ширина спектра 
Вернёмся к общему случаю
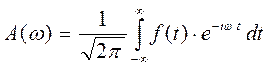
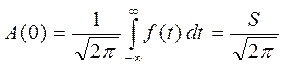
Пусть 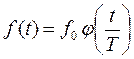 ,
, 
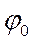 - амплитуда, Т – характерная ширина
- амплитуда, Т – характерная ширина
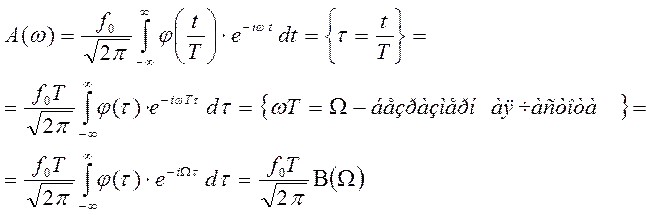
Общие выводы
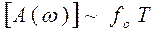
Если f - вольт, то спектр напряжение, А – вольт.сек.
Спектр морского волнения 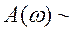 см. сек.
см. сек.


 |

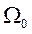
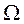
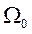 - эффективная ширина спектра
- эффективная ширина спектра
Но тогда 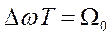
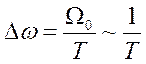 , как и в примерах
, как и в примерах
|
|
