💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Лекция 3

Итак, мы разложили в ряд Фурье по системе тригонометрических функций. Но это частный случай систем, по которым можно разложить произвольные функции. Еще одной из таких систем являются многочлены Лежандра (полиномы).

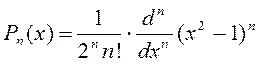, (n = 1, 2, …) на отрезке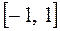

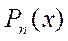- это многочлены степени n.

при n = 0 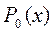= 1 (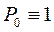 – это отдельно, не входит в n = 1, 2,.…).

n = 1 .

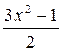n = 2 = =

= = =

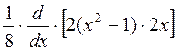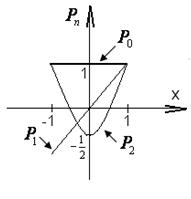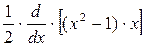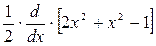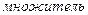
В общем случае

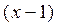
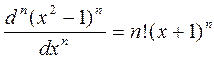+ … = (38)

здесь не выписаны члены, содержащие

множитель 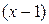, Покажем это.

Дифференцируя 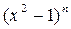= 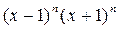по правилу Лейбница

= +

+ .

=

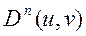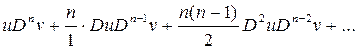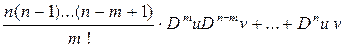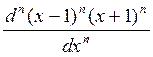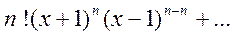
в данном случае n = m, т.е. n – n = 0, 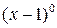= 1.

Т.о., общем случае

Т.е. мы видим, что это полиномы вида:

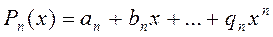
Докажем ортогональность системы полиномов.

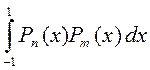при m < n

достаточно посмотреть

= =

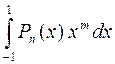интегрируя m раз по частям

= -

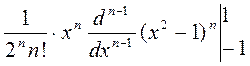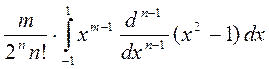
Первое слагаемое равно 0 потому, что 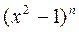имеет числа +1 и -1 своими нулями.

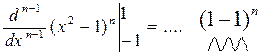
Интегрируя по частям m раз, получим так же 0, и так до (n – m) члена

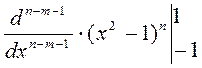= = 0.

Получили нули во всех слагаемых.

Полученные равенства показывают, что система полиномов Лежандра – ортогональна на [-1, 1].

Теперь о норме.

По определению

=

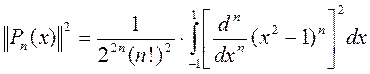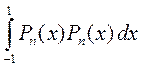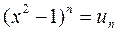обозначим

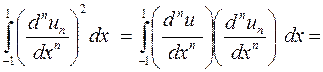= , но

возьмем его по частям

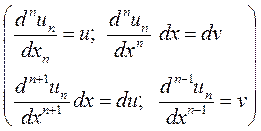
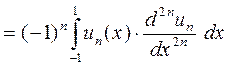
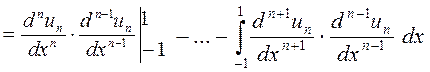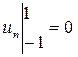
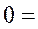
но, поскольку 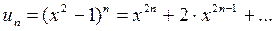, то

.

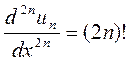Тогда

.

Интеграл

= = =

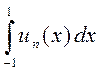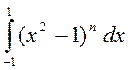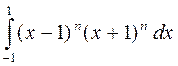интегрируя по частям, получим

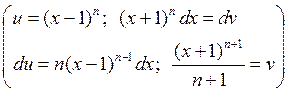
= 0

= - = … =

= = … = =

= = .

= .

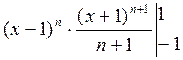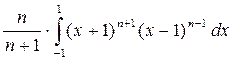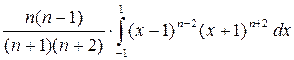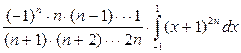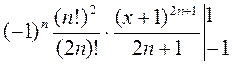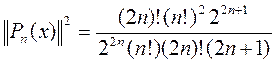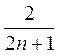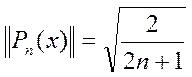(39)

Тогда нормированные многочлены имеют вид

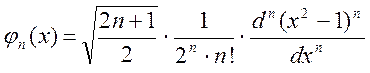(n = 0, 1, 2 …).

Можно показать, что если провести процесс ортогонализации системы

…

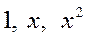на отрезке [-1, 1], то получим полную ортогональную и нормальную на [-1, 1] систему

…

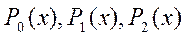К полиномам Лежандра применима общая теория ортогональных систем функций, т.е., в частности, наличие ортогональной системы функций позволяет разложить по ней произвольную функцию (в некоторый ряд Фурье)

,

Где вместо синусов и косинусов стоят полиномы Лежандра, причем области определения 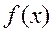и должны быть одинаковы, т.е. можно образовать пространство функций 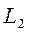(2-интегрируемости с квадратом) на интервале (a, b). Это тоже принципиально!.

Для нахождения коэффициентов 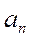надо

= = ,

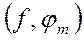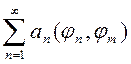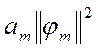откуда

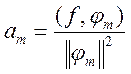
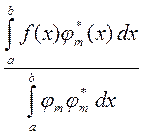= . (40)

коэффициенты ряда функции f по ортогональной системе функций (можно сказать, коэффициенты ряда Фурье).