
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Логарифмические неравенства.
|
|
Пусть а – фиксированное число такое, что 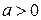 и
и 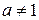 .
.
Рассмотрим неравенства
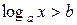 (1)
(1)
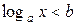 (2)
(2)
Областью допустимых значений этих неравенств является положительная полуось. Поскольку свойства логарифмической функции различны при основаниях, меньших и больших единицы, то рассмотрим случаи  и
и 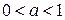 .
.
Пример.
Найти все значения а, при каждом из которых неравенство 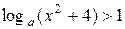 выполняется для всех х.
выполняется для всех х.
Решение.
Данное неравенство равносильно совокупности двух систем:
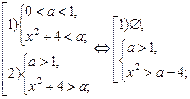
Система 1) не может выполняться ни при одном х, так как
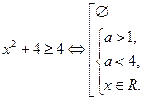
Ответ: 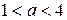 .
.
При решении логарифмических неравенств, содержащих несколько различных функций под знаком логарифмов, рекомендуется сначала найти область определения исходного выражения, и лишь затем совершать преобразования, в ходе которых область определения может сужаться или расширяться.
Пример.
Решить неравенство
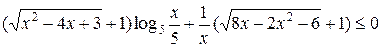 .
.
Решение.
Ключевым моментом в решении данного неравенства является поиск его области определения.
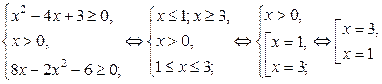
Выяснить, что область определения неравенства состоит только из двух точек.
Осталось подстановкой выяснить, какие из этих точек удовлетворяют неравенству.
При 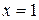 неравенство принимает вид
неравенство принимает вид 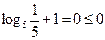 - истинно.
- истинно.
При 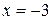 неравенство принимает вид
неравенство принимает вид 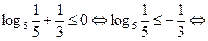
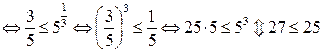 - ложно.
- ложно.
Ответ: 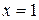 .
.
Пример.
Какое из двух чисел больше 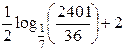 или
или  ?
?
Решение.
Упростим запись каждого из двух чисел:
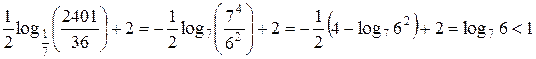 .
.
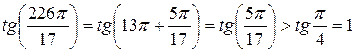 ,
,
Так как 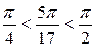 , и функция
, и функция 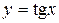 монотонно возрастает на
монотонно возрастает на 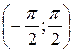 , получим, что первое число меньше 1, а второе число больше 1.
, получим, что первое число меньше 1, а второе число больше 1.
Ответ: 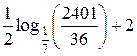 <
< 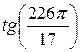 .
.
Рассмотрим неравенства вида
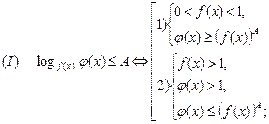
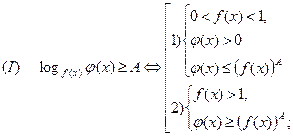
Пример. Решить неравенство
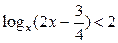
Решение.
Согласно схеме (I), заменим данное неравенство равносильной совокупностью:
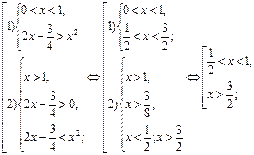
Ответ: 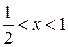 ,
, 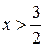 .
.
Пример. Решить неравенство
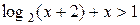
Решение.
Функция 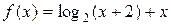 монотонно возрастает для
монотонно возрастает для 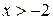 , как сумма двух монотонно возрастающих функций,
, как сумма двух монотонно возрастающих функций,  . Поэтому
. Поэтому 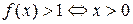 .
.
Ответ: 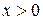
При решении неравенства воспользовались следующим утверждением:
Пусть функция 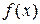 монотонно возрастает на промежутке Е, причем все ее значения на этом промежутке принадлежат Е, тогда неравенство примет вид:
монотонно возрастает на промежутке Е, причем все ее значения на этом промежутке принадлежат Е, тогда неравенство примет вид:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
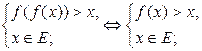
Следствие:

Покажем, как используются логарифмические неравенства для решения более сложных задач. Например, для нахождения области определения функции или множества значений данной функции.
Для нахождения области определения логарифмической функции 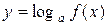 необходимо найти множество значений
необходимо найти множество значений 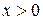 , при которых выполняется условие
, при которых выполняется условие 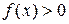 . Решение заданий с дополнительными требованиями «указать длину промежутка, на котором функция определена», «при каком целом значении х функция определена» сводится к двум этапам:
. Решение заданий с дополнительными требованиями «указать длину промежутка, на котором функция определена», «при каком целом значении х функция определена» сводится к двум этапам:
I этап – находят все значения х, при которых 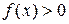 ;
;
II этап – делают выборку значений х из полученного промежутка согласно дополнительному требованию.
Пример.
Укажите длину промежутка области определения функции
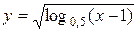 .
.
Решение.
1) Найдем значения х, при которых 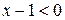 ,
, 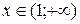

2) Найдем область определения функции
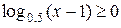 ,
,
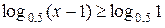 .
.
Далее по схеме 1, так как основание логарифма 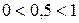 , то
, то
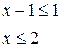
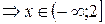

3) Объединяя полученные промежутки, получаем 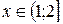 .
.
Таким образом, длина промежутка области определения данной функции равна 1.
Ответ: 1.
При нахождении области значений функции 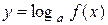 необходимо прежде всего найти множество значений функции
необходимо прежде всего найти множество значений функции 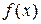 , а затем на основании свойства логарифмической функции
, а затем на основании свойства логарифмической функции 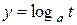 указать область значений
указать область значений 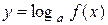 . Если в задании есть дополнительные требования, то решение будет состоять из трех этапов:
. Если в задании есть дополнительные требования, то решение будет состоять из трех этапов:
I этап – находим область значений 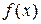 ;
;
II этап – находим область значений 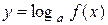 ;
;
III этап – выполняем дополнительные требования.
Пример.
Укажите наименьшее значение функции
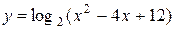
Решение.
1) Определим множество значений функции: 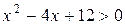 . Выделив полный квадрат, получим
. Выделив полный квадрат, получим
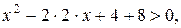
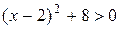 .
.
Так как 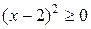 для всех действительных х, то
для всех действительных х, то 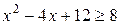 .
.
2) Таким образом, поскольку 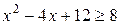 , а
, а 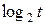 - возрастающая функция, то
- возрастающая функция, то
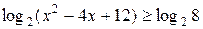 ,
,
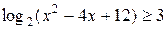 .
.
3) Область значений функции представляет собой луч 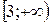 .
.
4) Наименьшее значение на этом луче равно 3.
Ответ: 3.
Покажем на примерах применение свойств логарифмической функции к решению неравенств.
Пример.
Решить 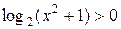 .
.
Решение.
Для наглядности решения построим график функции 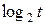 .
.
| t | 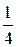
| 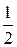
| ||||
| y | -2 | -1 |
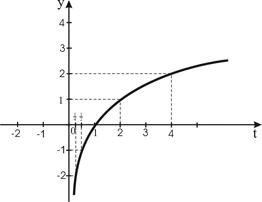
Из рисунка видно, что функция принимает положительные значения при 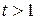 .
.
Далее, учитывая область определения функции 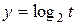 , получим:
, получим:
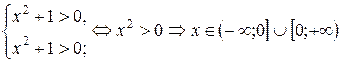
Ответ: 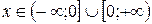 .
.
Изменяя знак неравенства, проследим за изменением получаемого результата.
Пример.
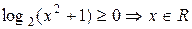

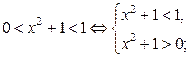
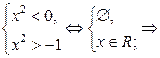 неравенство не имеет решений.
неравенство не имеет решений.
Логарифмические неравенства в общем виде решаются по схеме
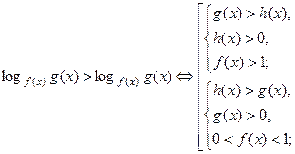
При замене на нестрогое логарифмическое неравенство нужно в совокупности систем первые неравенства менять на нестрогие, а остальные оставлять строгими.
Если попытки применить стандартные приемы не приводят к цели, то можно воспользоваться следующим утверждением:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Чтобы доказать, что на подмножестве 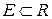 своей области определения неравенство
своей области определения неравенство 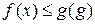 не имеет решений, достаточно, например, найти такую константу А, что для всех
не имеет решений, достаточно, например, найти такую константу А, что для всех 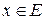 справедлива система неравенств
справедлива система неравенств
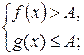 (*)
(*)
Наоборот, если на множестве Е выполняется система неравенств (*), то все точки этого множества удовлетворяют неравенству 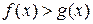 .
.
Задания:
1. Решите показательные неравенства:
Вариант 1 Вариант 2
а) 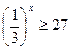 а)
а) 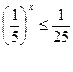
б) 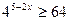 б)
б) 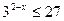
2. Решите логарифмические неравенства
Вариант 1 Вариант 2
а) 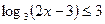 а)
а) 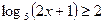
б) 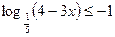 б)
б) 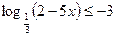
в) 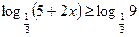 в)
в) 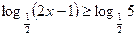
Контрольные вопросы:
1. Какие способы решения логарифмических уравнений вы знаете?
2. Какие способы решения показательных уравнений вы знаете?
|
|
