Пассивный и последовательный поиск

Пусть требуется найти наименьшее значение или точную нижнюю грань f *скалярной действительной функции f (x) одного переменного на отрезке [ а, b ]. Предположим, что задан алгоритм вычисления значения функции для любой точки х ∈ [ а, b ]. Можно выделить две группы методов прямого поиска, соответствующие двум принципиально различным ситуациям:

1) все N точек 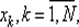в которых будут вычислены значения функции, выбирают заранее (до вычисления функции в этих точках);

2) точки xk выбирают последовательно (для выбора последующей точки используют значения функции, вычисленные в предыдущих точках).

В первом случае поиск значения f *называют пассивным, а во втором — последовательным. Естественно ожидать, что последовательный поиск лучше пассивного. В этом можно убедиться, вспомнив детскую игру, в которой надо найти спрятанную вещь, задавая вопросы и получая на них ответы «да» или «нет». Задавая вопросы последовательно с учетом предыдущих ответов, можно найти спрятанную вещь за меньшее число вопросов (итераций), чем задав определенное количество заранее подготовленных вопросов сразу.

Так как в прикладных задачах вычисление каждого значения функции может быть достаточно трудоемким, то целесообразно выбрать такую стратегию поиска, чтобы значение f *с заданной точностью было найдено наиболее экономным путем. Будем считать, что стратегия поиска определена, если:

— определен алгоритм выбора точек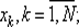

— определено условие прекращения поиска, т. е. условие, при выполнении которого значение f *считают найденным с заданной точностью.

Для методов пассивного поиска алгоритм выбора точек 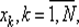— это правило, по которому заранее определяют все N точек 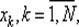в которых затем будут вычислены значения функции f (x). Для методов последовательного поиска алгоритм выбора точек х k — это правило, по которому последовательно определяют каждую следующую точку х k по информации о расположении точек 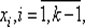и о вычисленных значениях f (х i) функции f (x) в этих точках. Выбор очередной точки xk и вычисление значения f (х k) называют шагом последовательного поиска.

В методах последовательного поиска количество точек х k обычно не задают заранее. Однако объективное сравнение различных методов прямого поиска нужно проводить при одинаковом количестве п вычисленных значений функции f (x). После n вычислений обычно указывают интервал (или отрезок) длины ln называемый интервалом неопределенности, в котором гарантированно находится точка х *, соответствующая значению f *. Условие прекращения вычислений в случае пассивного или последовательного поиска примем одинаковым — выполнение неравенства l п ≤ ε *, где ε *— заданная наибольшая допустимая длина интервала неопределенности.

Длина l п зависит как от самого метода прямого поиска Р, так и от минимизируемой функции f (x), т. е. ln = ln (P, f). Зависимость l п от п дает оценку скорости сходимости конкретного метода прямого поиска Р к искомому значению f *заданной функции f (х). Различные методы из некоторого множества Ƥ методов прямого поиска сравнивают обычно при выбранном фиксированном значении п = N на некотором достаточно широком классе функций. В качестве такого класса можно выбрать множество ℱ унимодальных функций, определенных на фиксированном отрезке X ⊂ ℝ. Для метода прямого поиска Р ∈ Ƥ примем наихудшую оценку

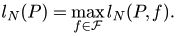
Если «наихудшей» унимодальной функции не найдется, то оценку принимаем в виде

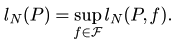
Значение ln (P) представляет собой оценку сверху погрешности вычисления точки х * ∈ X, соответствующей искомому значению f *произвольной функции f ∈ ℱ, которая получена методом прямого поиска Р ∈ Ƥ по N вычисленным значениям этой функции. Метод прямого поиска Р* считаем наилучшим, если

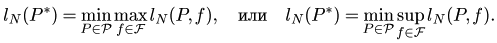
Этот критерий сравнения методов поиска определяет минимаксный метод поиска. Такой метод является наилучшим для всего множества ℱ унимодальных функций на отрезке X ⊂ ℝ в том смысле, что он дает наименьшую погрешность вычисления точки x *, соответствующей значению f *любой из рассматриваемых функций f ∈ ℱ. Хотя вполне возможно, что существует некоторый конкретный метод, который для определенной специально подобранной унимодальной функции из множества ℱ обеспечит еще меньшую погрешность.

Все методы прямого поиска можно строить и сравнивать между собой на отрезке X = [0, 1]. Полученные результаты при необходимости нетрудно перенести на случай произвольного отрезка [ а, b ], так как любую точку отрезка [0, 1] можно перевести в соответствующую ей точку отрезка [ а, b ] растяжением в b – а раз и сдвигом на а.

Если минимизируемая функция f (x) не является унимодальной на отрезке [ а, b ] (такую функцию называют мультимодальной функцией на этом отрезке), то, даже если она непрерывна на [ а, b ]), при поиске наименьшего значения f *функции на отрезке может возникнуть ошибка: будет найдена точка локального минимума, в которой значение функции не f *, а другое, большее. Чтобы избежать такой ошибки, в процесс минимизации включают предварительный этап, на котором отрезок минимизации разделяют на несколько отрезков, на каждом из которых минимизируемая функция унимодальна. Сравнительный анализ наименьших значений функции на этих отрезках позволяет найти искомое наименьшее значение f * на всем отрезке минимизации.

Пример 2.1. Рассмотрим один из возможных подходов к выделению из промежутка X в области определения D (f) минимизируемой функции f (x) отрезка [ а, b ], на котором эта функция является унимодальной. Пусть известна такая точка x 0∈ X, что при х ≥ x 0функция f (x) сначала убывает, а затем начиная с пока неизвестного значения х = x * ∈ X возрастает, хотя далее в промежутке X могут быть расположены и другие участки немонотонного поведения этой функции. Выберем начальное значение h > 0 приращения аргумента x функции f (x), в несколько раз меньшее предполагаемого расстояния между точками x 0и x *, и вычислим значения f (x 0) и f (x 1), где x 1= x 0+ h.

Может оказаться, что f (x 0) ≤ f (x 1). Тогда за искомый отрезок [ а, b ] можно сразу принять отрезок [ x 0, x 1]. Но можно продолжить вычисления и, используя последовательный поиск, определять значения f (xk) в точках xk = x 0+ h / 2 k – 1, k = 2, 3..., до тех пор, пока не будет выполнено неравенство f (xk) ≤ f (x 0). Тогда следует принять [ а, b ] = [ x 0, xk – 1 ] (на рис.. 2.2 [ а, b ] = [ x 0, x 2], поскольку точка x *должна быть либо на отрезке [ x 0, x 3], либо на отрезке [ x 3, x 2]. Надо сказать, что при этом можно „не заметить" по крайней мере еще один отрезок, на котором функция унимодальна (штриховая линия на рис. 2.2).

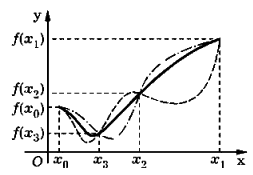
Рис. 2.2

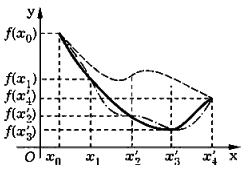
Рис. 2.3

Если f (x 0) > f (x 1), то, используя последовательный поиск, вычисляем значения f (x ' k), где x ' k = x 0+ (k – l) h. k = 2, 3... пока не будет выполнено неравенство f (x ' k – 1) ≤ f (x ' k), что позволяет принять [ а, b ] = [ x ' k – 2, x ' k ] (на рис. 2.3 [ а, b ] = [ х '2, х '4], так как точка x *должна быть либо на отрезке [ х '2, х '3], либо на отрезке [ х '3, х '4]).

Отметим, что описанный подход не гарантирует нахождения отрезка унимодальности функции. Например, на рис. 2.3 штриховой линией показан график функции, для которой этот подход не позволяет обнаружить искомый отрезок.

Метод золотого сечения. Как известно, золотым сечением отрезка называют такое его деление на две неравные части, при котором отношение длины всего отрезка к длине его большей части равно отношению длины большей части к длине меньшей.

Термин «золотое сечение» ввел Леонардо да Винчи. Золотое сечение широко применяли при композиционном построении многих произведений мирового искусства, в том числе в античной архитектуре и в эпоху Возрождения.

Рассмотрим k - й шаг последовательного поиска. Чтобы выполнить процедуру исключения отрезка на этом шаге, отрезок [ а k, bk ] необходимо двумя внутренними точками xk 1, х k 2, xk 1< х k 2, разделить на три части. Эти точки выберем симметрично относительно середины отрезка [ а k, bk ] (рис. 2.8) и так, чтобы каждая из них производила золотое сечение отрезка [ а k, bk ]. В этом случае отрезок [ а k + 1, bk + 1 ] внутри будет содержать одну из точек xk 1, х k 2(другая будет одним из концов отрезка), причем эта точка будет производить золотое сечение отрезка [ а k + 1, bk + 1 ]. Это вытекает из равенства длин отрезков [ а k, xk 1] и [ xk 2, bk ]. Таким образом, на (k + 1)-м шаге в одной из точек xk + 1, 1, xk + 1, 2 значение функции вычислять не нужно. При этом отношение lk / lk + 1 длин отрезков сохраняется от шага к шагу, т. е.

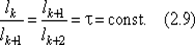
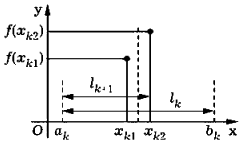
Рис. 2.8

Число τ называют отношением золотого сечения.

Последовательный поиск, в котором на k -м шаге каждая из симметрично выбранных на отрезке [ а k, bk ] точек xk 1, xk 2осуществляет золотое сечение этого отрезка, называют методом золотого сечения. В этом методе каждое исключение отрезка уменьшает оставшийся отрезок в τ раз.

Выясним, чему равно отношение золотого сечения. Так как точки xk 1и xk 2, xk 1< xk 2, выбраны симметрично относительно середины отрезка [ а k, bk ], то

bk – xk 2= xk 1– а k = lk – lk + 1

(см. рис. 2.8). Для определенности будем считать, что на k -м шаге выбран отрезок [ а k, xk 2]. Тогда на (k + 1)-м шаге одной из точек деления (а именно правой) будет точка xk 1. Значит, длина lk + 2 отрезка, выбираемого на (к + 1)-м шаге, совпадает с длиной отрезка [ a, xk 1] и верно равенство lk + 2 = lk – lk + 1. Подставляя найденное выражение для lk + 2 в уравнение (2.9), получаем

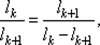
или τ = 1 / (τ – 1). Преобразуя это соотношение, приходим к квадратному уравнению τ 2– τ – 1 = 0, имеющему единственное положительное решение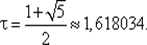