Методы обобщенного покоординатного спуска

Пусть решается задача J (х) → min, х ∈ R n, J ∈ (C 2(R n) с овражным… функционалом. Основной процедурой при реализации рассматриваемого далее класса методов обобщенного покоординатного спуска (ОПС) является процедура диагонализации матрицы J " (x) с последующим циклическим покоординатным спуском вдоль собственных векторов. Целесообразность такого подхода вытекает из геометрически очевидного факта, заключающегося в том, что оси наиболее рациональной системы координат при минимизации квадратичных функционалов (независимо от их выпуклости) методом покоординатного спуска совпадают с собственными векторами матрицы вторых производных, являющихся осями симметрии соответствующих поверхностей уровня. Эта идея неоднократно высказывалась в литературе, и даже строились соответствующие алгоритмы. Однако численные эксперименты показали низкую эффективность такого подхода. Существует и объяснение этих неудовлетворительных результатов. Оно основано на том, что при определении собственных векторов, соответствующих близким или кратным собственным значениям, возникают принципиальные вычислительные трудности. Аналогичные трудности, связанные с ограниченной точностью задания исходной информации, а также последующих вычислений, наблюдаются и при диагонализации плохо обусловленных матриц, имеющих относительно малые по модулю спектральные составляющие. Указанные обстоятельства, по-видимому, явились основным сдерживающим фактором, не позволившим внедрить изучаемые далее методы в вычислительную практику. Однако из дальнейшего изложения следует, что неудачи при численном экспериментировании были вызваны, по-видимому, особенностями реализации метода, рассчитанной на случай выпуклых функционалов. Как показано далее, для целей оптимизации, как в выпуклой ситуации, так и в невыпуклой, достаточно вычислить произвольный ортонормированный базис в инвариантном подпространстве, отвечающем каждой изолированной группе собственных значений. При этом собственные векторы могут быть вычислены со значительными погрешностями.

Отвечающие этим базисам линейные оболочки с высокой точностью совпадают с истинными подпространствами, определяемыми невозмущенной диагонализируемой матрицей.

Этот вывод в известной степени подтверждаются следующей теоремой.

Теорема 4.1. Пусть А — симметричная матрица п × п; { и i } — ортонормированные собственные векторы; λ i — собственные значения. Тогда при λ i ≠ λ j с точностью до величин второго порядка малости имеем

где dA — возмущение матрицы А; du i — соответствующее возмущение вектора ui.

Изложенное позволяет в качестве модели программ, реализующих различные методы диагонализации матрицы A, использовать оператор Λ (A), ставящий в соответствие произвольной симметричной матрице А ортогональную матрицу V, отличную, вообще говоря, от истинной матрицы U, состоящей из собственных векторов матрицы А. Оператор Л характеризуется тем, что если спектр матрицы А разделяется на р групп

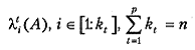
«близких» между собой собственных чисел, то каждой группе соответствует набор столбцов { v it } матрицы V, задающий точное линейное многообразие, порожденное соответствующими столбцами { u i } точной матрицы U.

Рассмотрим квадратичную аппроксимацию

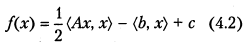
исходного функционала J (х) в окрестности точки х ∈ Q. Допустим, что известны матрица А и ортогональная матрица U, приводящая ее к диагональному виду U T AU = diag λ i. Тогда замена переменных х = Uy приводит квадратичный функционал к сепарабельному виду

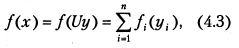
где f i — квадратичные функции одной переменной (параболы). Таким образом достигается полная локальная декомпозиция исходной задачи, и последняя сводится к п независимым экстремальным задачам. В результате поиск оптимального вектора у * может осуществляться покомпонентно, так как связь между аргументами у i фактически исчезает. В указанной идеализированной ситуации явление заклинивания метода покоординатного спуска невозможно, и все вычислительные проблемы при применении покоординатных стратегий поиска оптимума, связанные с большими значениями η, формально снимаются.

В действительности бывает задана не матрица A, а возмущенная матрица А + dA, где dA отражает как неопределенность задания исходной матрицы A, так и последующие ошибки округления при проведении собственно процесса диагонализации. В связи с этим вместо точной матрицы U оказывается доступной некоторая матрица V = Λ (A). Замена переменных х = Vy уже не приводит к представлению (4.3). Для изучения создавшейся ситуации важное значение имеет следующая теорема.

Теорема 4.2. Пусть собственные значения { λ i } и отвечающие им ортонормированные собственные векторы { ui }, i ∈ [1: п ] некоторой симметричной матрицы А разделены произвольным образом на р групп 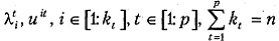так, что означают j -e собственное число и соответствующий собственный вектор группы t. Тогда, если в каждом линейном многообразии М t размерности 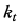с базисом 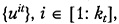задать иной ортонормированный базис 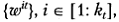связанный с исходным базисом линейным соотношением

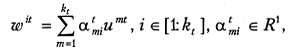
то существует такая матрица Р перестановок столбцов, что:

1) преобразование подобия 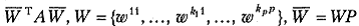приводит матрицу А к блочно-диагональному виду 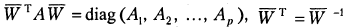с квадратными 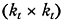матрицами At на главной диагонали;

2) собственные значения матрицы At есть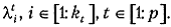

Теорема 4.3. Пусть V= Λ (A), тогда

1) замена переменных x=Vy с точностью до нумерации компонентов вектора у приводит функционалах) (4.2) к блочно-сепарабельному виду

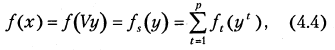
где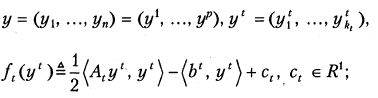

2) собственные значения матрицы равны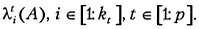

Следствие. Пусть собственные числа матрицы А удовлетворяют неравенствам λ 1 ≥ … ≥ λ n – r > > | λ n – r + 1 | ≥ … ≥ | λ n |, тогда

1) замена переменных х = Vy, V = Λ (A), где V = (v 11,..., v 1 n – r, v 21,..., v 2 r)T;

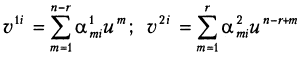
с точностью до нумерации компонентов вектора у приводит f (x) к виду

fs (у) = f 1(y 1) + f 2(y 2), y = (y 1, у 2), (4.5)

где у 1= (у 1, ..., y п – r), у 2= (y п – r + 1, ..., y п);

2) η 1< < η, η 2< < η, где η i — показатели овражности задач fi → min, i = 1, 2.

Таким образом, исходная оптимизационная задача локально может быть сведена к двум эквивалентным задачам с существенно меньшими числами η i. Представление (4.5) реализует принцип частичной локальной декомпозиции и является аналогом идеализированного соотношения (4.3).

Если собственные числа матрицы квадратичного функционала разделяются более чем на две группы, то будет справедливо представление (4.5), содержащее соответствующее число слагаемых.

Согласно (4.5), появляется возможность независимого решения не связанных между собой оптимизационных задач для функционалов fi с невысокими показателями овражности.

Полученные результаты носят локальный характер и справедливы в рамках квадратичной аппроксимации исходного функционала J (х). Для неквадратичных функционалов приближенное выполнение соотношений типа (4.5) позволяет говорить о существенном ослаблении связей между различными группами переменных, что определяет достаточно высокую эффективность покоординатного спуска и в общем случае.