Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

АЛГОРИТМ ДИФФі-ХЕЛЛМАНА

Припустимо, що обом абонентам відомі деякі два числа g і p (наприклад, вони можуть бути «зашиті» в програмне забезпечення), які не є секретними і можуть бути відомі також іншим зацікавленим особам. Для того, щоб створити невідомий більш нікому секретний ключ, обидва абонента генерують великі випадкові числа: перший абонент — число a, другий абонент — число b. Потім перший абонент обчислює значення A = gamod p і пересилає його друга, а другий обчислює B = gbmod p і передає першому.

Передбачається, що зловмисник може отримати обидва цих значення, але не модифікувати їх (тобто у нього немає можливості втрутитися в процес передачі). На другому етапі першого абонент на основі наявної в нього a і отриманого по мережі B обчислює значення Bamod p = gabmod p, а другий абонент на основі наявної в нього b і отриманого по мережі A обчислює значення Abmod p = gabmod p. Як неважко бачити, у обох абонентів вийшло одне і те ж число: K = gabmod p. Його вони і можуть використовувати в якості секретного ключа, оскільки тут зловмисник зустрінеться з практично нерозв’язною (за розумний час) проблемою обчислення gabmod p по перехоплених gamod p і gbmod p, якщо числа p, a, b обрані досить великими.

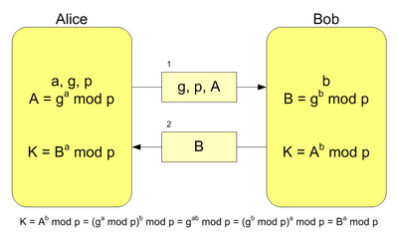
Під час роботи алгоритму, кожна сторона:

1. генерує випадкове натуральне число a — закритий

2. спільно з віддаленої стороною встановлює відкриті параметри p і g (зазвичай значення p і g генеруються на одній стороні і передаються іншій), де
p є випадковим простим числом
g є первісним коренем за модулем p

3. обчислює відкритий ключ A, використовуючи перетворення над закритим ключем
A = ga mod p

4. обмінюється відкритими ключами з віддаленої стороною

5. обчислює загальний секретний ключ K, використовуючи відкритий ключ віддаленої сторони B і свій закритий ключ a
K = Ba mod p
До виходить рівним з обох сторін, тому що:
Ba mod p = (gb mod p) a mod p = gab mod p = (ga mod p) b mod p = Ab mod p.