
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Огляд існуючих методів рішення
|
|
Для того, щоб створити новий метод шифрування, необхідно зробити огляд вже існуючих шифрів, взяти з них найкращі ідеї, додати свої і скомпонувати. Але перед цим потрібно зрозуміти що таке криптографія, її загальні визначення та класифікація, а також технологія захисту інформації.
Криптографія (від грецького kryptоs – прихований і grаphein – писати) – наука про математичні методи забезпечення конфіденційності (неможливості прочитання інформації стороннім) і автентичності (цілісності і справжності авторства) інформації. Розвинулась з практичної потреби передавати важливі відомості найнадійнішим чином.
Криптографія займалася виключно забезпеченням конфіденційності повідомлень (тобто шифруванням) — перетворенням повідомлень із зрозумілої форми в незрозумілу і зворотнє відновлення на стороні одержувача, роблячи його неможливим для прочитання для того, хто перехопив або підслухав без секретного знання (а саме ключа, необхідного для дешифровки повідомлення). В останні десятиліття сфера застосування криптографії розширилася і включає не лише таємну передачу повідомлень, але і методи перевірки цілісності повідомлень, ідентифікування відправника/одержувача (аутентифікація), цифрові підписи, інтерактивні підтвердження, та технології безпечного спілкування, тощо.
Для сучасної криптографії характерне використання відкритих алгоритмів шифрування, що припускають використання обчислювальних засобів. Відомо більш десятка перевірених алгоритмів шифрування, які, при використанні ключа достатньої довжини і коректної реалізації алгоритму, роблять шифрований текст недоступним для крипто аналізу.
Криптографія є найпотужнішим на сьогоднішній день засобом захисту інформації. Вона зародилася майже одночасно із самим мистецтвом письма і на сьогоднішній день перетворилася на могутню прикладну науку, засновану на глибоких математичних знаннях. Проти самого криптографічного захисту не допомагають ні різні хитрощі, ні використання самих потужних електронно-обчислювальних машин (ЕОМ) світу – тут на сторожі таємниць стоїть математика. Єдиною можливістю для зловмисника є обхідні шляхи, такі як крадіжка діючих і використаних ключів, передбачення майбутніх значень генераторів псевдовипадкових чисел.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Криптографічні ключі розрізняються згідно алгоритмам, в яких вони використовуються.
· Секретні (Симетричні) ключі – ключі, що використовуються в симетричних алгоритмах (шифрування, вироблення кодів автентичності). Головна властивість симетричних ключів: для виконання як прямого, так і зворотного криптографічного перетворення (шифрування / розшифрування,) необхідно використовувати один і той же ключ (або ж ключ для зворотного перетворення легко обчислюється із ключа для прямого перетворення, і навпаки). З одного боку, це забезпечує більш високу конфіденційність повідомлень, з іншого боку, створює проблеми розповсюдження ключів в системах з великою кількістю користувачів.
· Асиметричні ключі – ключі, що використовуються в асиметричних алгоритмах (шифрування); складаються з двох ключів (ключова пара):
§ Закритий ключ (en: Private key) – ключ, відомий тільки своєму власнику. Тільки збереження користувачем у таємниці свого закритого ключа гарантує неможливість підробки зловмисником документа і цифрового підпису від імені котрий запевняє.
§ Відкритий ключ (en: Public key) – ключ, який може бути опублікований і використовується для перевірки дійсності підписаного документа, а також для попередження шахрайства з боку посвідчує особи у вигляді відмови його від підпису документа. Відкритий ключ підпису обчислюється, як значення деякої функції від закритого ключа, але знання відкритого ключа не дає можливості визначити закритий ключ.
Симетричні криптосистеми володіють одним серйозним недоліком. Пов’язано це із ситуацією, коли спілкування між собою провадять не три-чотири особи, а сотні й тисячі людей. У цьому випадку для кожної пари, що листується між собою, необхідно створювати свій секретний симетричний ключ. Це в підсумку приводить до існування в системі з N користувачів N2/2 ключів. А це вже дуже «пристойне» число. Крім того, при порушенні конфіденційності якої-небудь робочої станції зловмисник одержує доступ до всіх ключів цього користувача й може відправляти, ніби від його імені, повідомлення всім абонентам, з якими «жертва» вела переписку.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Своєрідним рішенням цієї проблеми стала поява асиметричної криптографії. Ця область криптографії дуже молода в порівнянні з іншими представниками. Перша схема, що мала прикладну значимість, була запропонована всього близько 30 років тому. Але за цей час асиметрична криптографія перетворилася в один з основних напрямків криптології, і використовується в сучасному світі також часто, як і симетричні схеми.
Асиметрична криптографія задумана як засіб передачі повідомлень від одного об’єкта до іншого (а не для конфіденційного зберігання інформації, що забезпечують тільки симетричні алгоритми). Тому приймаємо терміни «відправник» – особа, що шифрує, а потім відправляє інформацію з незахищеного каналу й «одержувач» – особа, що приймає й відновлює інформацію в її вихідному вигляді. Основна ідея асиметричних криптоалгоритмів полягає в тому, що для шифрування повідомлення використається один ключ, а при дешифруванні – інший.
Крім того, процедура шифрування обрана так, що вона необоротна навіть за відомим ключем шифрування – це друга необхідна умова асиметричної криптографії. Тобто, знаючи ключ шифрування й зашифрований текст, неможливо відновити вихідне повідомлення – прочитати його можна тільки за допомогою другого ключа – ключа дешифрування. А якщо так, то ключ шифрування для відправлення листів якій-небудь особі можна взагалі не приховувати – знаючи його однаково неможливо прочитати зашифроване повідомлення. Тому, ключ шифрування називають в асиметричних системах «відкритим ключем», а от ключ дешифрування одержувачеві повідомлень необхідно тримати в секреті – він називається «закритим ключем». Напрошується питання: «Чому, знаючи відкритий ключ, не можна обчислити закритий ключ?» – це третя необхідна умова асиметричної криптографії – алгоритми шифрування й дешифрування створюються так, щоб знаючи відкритий ключ, неможливо обчислити закритий ключ.
В цілому система переписки при використанні асиметричного шифрування виглядає в такий спосіб. Для кожного з Nабонентів, що ведуть переписку, обрана своя пара ключів: «відкритий» Ej й «закритий» Dj, де j – номер абонента. Всі відкриті ключі відомі всім користувачам мережі, кожен закритий ключ, навпаки, зберігається тільки в того абонента, якому він належить. Якщо абонент, скажемо під номером 7, збирається передати інформацію абонентові під номером 9, він шифрує дані ключем шифрування E9 і відправляє її абонентові 9. Незважаючи на те, що всі користувачі мережі знають ключ E9 й, можливо, мають доступ до каналу, яким йде зашифроване послання, вони не можуть прочитати вихідний текст, тому що процедура шифрування необоротна за відкритим ключем. І тільки абонент 9, одержавши послання, робить над ним перетворення за допомогою відомого тільки йому ключа D9 і відновлює текст послання. Помітьте, що якщо повідомлення потрібно відправити в протилежному напрямку (від абонента 9 до абонента 7), то потрібно буде використати вже іншу пару ключів (для шифрування ключ E7, а для дешифрування – ключ D7).
Симетричні криптоалгоритми поділяються на:
1. Потокові шифри – побітна обробка інформації. Шифрування і дешифрування в таких схемах може обриватися в довільний момент часу, як тільки з’ясовується, що потік що передається перервався, і також відновлюється при виявленні факту продовження передачі.
1.1 Скремблер – це набір біт, які міняються на кожному кроці по визначеному алгоритму. Після виконання кожного наступного кроку на його виході з’являється шифруючий біт (0 або 1), який накладається на поточний біт.
2. Блочні шифри – перетворення блоку вхідної інформації фіксованої довжини. Схема застосовується при пакетній передачі інформації та кодування файлів.
2.1 Мережа Фейштеля – метод оборотних перетворень тексту, при якому значення, обчислені від однієї з частин тексту, накладається на інші частини. Часто структура мережі виконується таким чином, що для шифрування і дешифрування використовується один і той же алгоритм – різниця полягає лише в порядку використання матеріалу ключа.
В основному, симетричні алгоритми шифрування вимагають менше обчислень, ніж асиметричні. На практиці, це означає, що якісні асиметричні алгоритми в сотні або в тисячі разів повільніші за якісні симетричні алгоритми. Недоліком симетричних алгоритмів є необхідність мати секретний ключ з обох боків передачі інформації. Так як ключі є предметом можливого перехоплення, їх необхідно часто змінювати та передавати по безпечних каналах передачі інформації під час розповсюдження.
Переваги:
— Швидкість
— Простота реалізації (за рахунок більш простих операцій)
— Необхідна менша довжина ключа для порівнянної стійкості
— Вивченість (за рахунок більшого віку)
Недоліки:
— Складність управління ключами у великій мережі. Це означає квадратичне зростання числа пар ключів, які треба генерувати, передавати, зберігати і знищувати в мережі. Для мережі в 10 абонентів потрібно 45 ключів, для 100 вже 4950, для 1000 – 499500.
— Складність обміну ключами. Для застосування необхідно вирішити проблему надійної передачі ключів кожному абоненту, тому що потрібен секретний канал для передачі кожного ключа обом сторонам.
Для компенсації недоліків симетричного шифрування в даний час широко застосовується комбінована (гібридна) криптографічний схема, де за допомогою асиметричного шифрування передається сеансовий ключ, що використовується сторонами для обміну даними за допомогою симетричного шифрування.
Важливою властивістю симетричних шифрів є неможливість їх використання для підтвердження авторства, так як ключ відомий кожній стороні.
Найпоширеніші методи шифрування:
Шифр Цезаря
Шифр Цезаря — симетричний алгоритм шифрування підстановками. Використовувався римським імператором Юлієм Цезарем для приватного листування.
Принцип дії полягає в тому, щоб циклічно зсунути алфавіт, а ключ — це кількість літер, на які робиться зсув.
Якщо зіставити кожному символу алфавіту його порядковий номер (нумеруючи з 0), то шифрування і дешифрування можна виразити формулами:
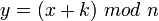
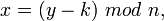
де 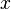 — символ відкритого тексту,
— символ відкритого тексту, 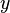 — символ шифрованого тексту,
— символ шифрованого тексту, 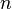 — потужність алфавіту, а
— потужність алфавіту, а 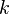 — ключ.
— ключ.
Можна помітити, що суперпозиція двох шифрувань на ключах 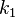 і
і 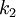 є просто шифруванням на ключі
є просто шифруванням на ключі  . Більш загально, множина шифруючих перетворень шифру Цезаря утворює групу
. Більш загально, множина шифруючих перетворень шифру Цезаря утворює групу 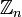 .
.
Шифр Цезаря має замало ключів — на одиницю менше, ніж літер в абетці. Тому перебрати усі ключі не складає особливої роботи. Дешифрування з одним з ключів дасть нам вірний відкритий текст.
Також зламати шифр Цезаря також можна, як і звичайний підстановочний шифр, у зв’язку з тим, що частота появи кожної літери в шифртексті збігається з частотою появи у відкритому тексті. Якщо припустити, що частота появи літер у відкритому тексті приблизно відповідає середньостатистичній відносній частоті появи літер в текстах мови, на якій написано повідомлення, тоді ключ знаходиться зіставленням перших декількох літер, що трапляються найчастіше у відкритому та зашифрованому текстах. Тобто за допомогою методу частотного криптоаналізу.
Шифр Віженера:
поліалфавітний шифр, який у якості ключа використовує слово. Ключове слово повторюється, поки не отримано гаму, рівну довжині повідомлення.
Отримав назву на честь Блеза де Виженера. Ci = (Pi + Kj) mod 33 (Pі, Kj, Ci – місце в алфавіті виражене через цифри). Сі – буква, яку потрібно зашифрувати, Рі – буква по верхньому ряду, Кі – буква по нижньому ряду таблиці.
| _ | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я |
| а | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я |
| б | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а |
| в | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б |
| г | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в |
| ґ | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г |
| д | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ |
| е | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д |
| є | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е |
| ж | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є |
| з | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж |
| и | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з |
| і | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и |
| ї | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і |
| й | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї |
| к | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й |
| л | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к |
| м | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л |
| н | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м |
| о | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н |
| п | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о |
| р | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п |
| с | с | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р |
| т | т | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с |
| у | у | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т |
| ф | ф | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у |
| х | х | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф |
| ц | ц | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х |
| ч | ч | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц |
| ш | ш | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч |
| щ | щ | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш |
| ь | ь | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ |
| ю | ю | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь |
| я | я | а | б | в | г | ґ | д | е | є | ж | з | и | і | ї | й | к | л | м | н | о | п | р | с | т | у | ф | х | ц | ч | ш | щ | ь | ю |
По вертикалі вибираємо літери відкритого тексту, а по горизонталі — ключа, на перетині цих значень отримуємо знаки шифротексту. Наприклад:
Відкритий текст: «полі/алфа/вітн/ий ши/фр»
Ключ: «ключ/ключ/ключ/кл юч/кл»
Шифротекст: «аайд/кьтч/мцрі/фш цґ/дв».
Шифр Вермана:
у криптографії, система шифрування, винайдена в 1917 році співробітниками AT& T Мейджором Джозефом Моборном і Гільбертом Вернамом.
Для відтворення шифртексту відкритий текст об'єднується операцією «виключне АБО» з ключем (названим одноразовим блокнотом або шифроблокнотом). При цьому ключ повинен володіти трьома критично важливими властивостями:
1. Бути справді випадковим;
2. Збігатися з розміром з заданим відкритим текстом;
3. Застосовуватися тільки один раз.
Шифр названий на честь телеграфіста AT& T Гільберта Вернама, що в 1917 році побудував телеграфний апарат, який виконував цю операцію автоматично - треба було тільки подати на нього стрічку з ключем. Не будучи шифрувальником, тим не менше, Вернам вірно помітив важливу властивість свого шифру - кожна стрічка повинна використовуватися тільки один раз і після цього знищуватися.
В 1949 році Клод Шеннон опублікував роботу, в якій довів абсолютну стійкість шифру Вернама. Інших шифрів з цією властивістю не існує. Це по суті означає, що шифр Вернама є найбезпечнішою криптосистемою з усіх можливих. При цьому умови, яким повинен задовольняти ключ, настільки сильні, що практичне використання шифру Вернама є важко здійсненним. Тому він використовується тільки для передачі повідомлень найвищої секретності.
На початку 20 ст. для передачі повідомлень все ширше і ширше використовувалися телетайпи. Тому потрібні були методи, що дозволяють шифрувати текст не до того, як він потрапляє до телеграфіста, а безпосередньо в момент передачі, і, відповідно, розшифровувати в момент прийому.
Подальше вдосконалення методу, запропонованого Вернамом, належить майбутньому начальнику зв'язку військ США Джозеф Моборну, що об'єднав хаотичність «гами», на яку спирався Вернам у своїй системі «автоматичного шифрування», з використовуваним у той час у військах правилом «одноразового шифрблокнота». Ідея Моборна полягала в тому, що кожна випадкова «гама» повинна використовуватися один, і тільки один раз. При цьому для шифрування кожного знака всіх текстів, які вже передані або будуть передані в найближчому майбутньому, повинен застосовуватися абсолютно новий і такий, що не піддається передбаченню знак «гами».
На практиці можна один раз фізично передати носій інформації з довгим дійсно випадковим ключем, а потім по мірі необхідності пересилати повідомлення. На цьому заснована ідея шифроблокнотів: шифрувальник при особистій зустрічі забезпечується блокнотом, кожна сторінка якого містить ключ. Такий же блокнот є і у приймаючої сторони. Використані сторінки знищуються.
Крім того, якщо є два незалежних канали, в кожному з яких ймовірність перехоплення низька, але відрізняється від нуля, шифр Вернама також можна застосувати: по одному каналу можна передати зашифроване повідомлення, по другому - ключ. Для того, щоб розшифрувати повідомлення, перехоплювач повинен прослуховувати обидва канали.
Шифр Вернама може застосовуватися, якщо є односторонній захищений канал: ключ передається в одну сторону під захистом каналу, повідомлення в іншу сторону захищаються ключем.
У період між двома світовими війнами в більшості країн з'являються електромеханічні шифратори. Вони були двох типів. Перший - пристрій, що складається з комутаційних дисків та механізму зміни їх кутових положень. За обома сторонами комутаційного диска розміщені контакти, відповідні алфавіту відкритого та шифрованого тексту. Контакти ці з'єднуються між собою відповідно до деякого правила підстановки, що зветься комутацією диска. Ця комутація визначає заміну літер в початковому кутовому положенні. При зміні кутового положення диска змінюється і правило підстановки. Таким чином, ключ шифрування містить кілька невідомих: схему з'єднання контактів і початкове кутове положення. Якщо після шифрування кожної літери міняти кутове положення диска - отримаємо багато алфавітне шифрування. Ще більш складний пристрій отримаємо, з'єднавши послідовно кілька дисків, кутові положення яких змінюються з різною швидкістю.
Широко відома шифрмашина «Енігма», якою були оснащені німецькі війська часів Другої світової війни, є типовим прикладом пристрою на комутаційних дисках. Конструктивно «Енігма» походила на звичайну друкарську машинку, тільки натискання клавіші призводило не до удару молоточка по паперу, а створювало електричний імпульс, що надходив у схему криптоперетворення. Американська шифрмашина М-209 - типовий приклад другого типу шифратора.
Таким чином, перед Другою світовою війною всі провідні країни мали на озброєнні електромеханічні шифрсистеми, що володіють високою швидкістю обробки інформації і високою стійкістю. Вважалося, що застосовувані системи неможливо розшифрувати і криптоаналізу більше робити абсолютно нічого. Як часто буває, ця думка була згодом спростована, і дешифровщики були безпосередніми учасниками бойових дій.
Завдяки накладеним обмеженням на ключ, в 1949 році Клод Шенон довів, що шифр Вернама є абсолютно криптостійким. Але:
1. Для роботи шифру Вернама необхідна дійсно випадкова послідовність нулів та одиниць (ключ). За визначенням, послідовність, отримана з використанням будь-якого алгоритму, є не зовсім випадковою, а псевдовипадковою. Тобто, потрібно отримати випадкову послідовність неалгорітмічно (наприклад, використовуючи радіоактивний розпад ядер, створений електронним генератором білий шум або інші досить випадкові події).
2. Проблемою є таємна передача послідовності та збереження її в таємниці. Якщо існує надійно захищений від перехоплення канал передачі повідомлень, шифри взагалі не потрібні: секретні повідомлення можна передавати з цього каналу. При цьому, оскільки довжина ключа така ж, як і довжина повідомлення, передати його не простіше, ніж повідомлення. Шифроблокнот на фізичному носії можна вкрасти або скопіювати.
3. Можливі проблеми з надійним знищенням використаної сторінки. Цьому схильні як паперові сторінки блокнота, так і сучасні електронні реалізації з використанням компакт-дисків або флеш-пам'яті.
4. Якщо третя сторона якимось чином дізнається повідомлення, вона легко відновить ключ і зможе підмінити повідомлення на інше такої ж довжини.
5. Шифр Вернама чутливий до будь-якого порушення процедури шифрування. Наприклад, контррозвідка США часто розшифровувала радянські та німецькі послання через неточності генератора випадкових чисел. Бували випадки, коли одна і та ж сторінка блокнота застосовувалася двічі - США також розшифровували такі послання.
Наприклад:
Слово " Москаленко" ключ 57065
1 листок: 38902...
2 листок: 57065 23252 82110 22152 42125
3 листок: 23056...
Текст " привет мир" ключ 57065
1 листок: 28763...
2 листок: 73521...
3 листок: 57065 26271 91215 29432 31927
Кодування алфавіту виконуватиметься в такій послідовності: 0 – 00…, 9 – 09…, а – 10…, я – 43.
RSA
RSA— криптографічна система з відкритим ключем.
RSA став першим алгоритмом такого типу, придатним і для шифрування і для цифрового підпису. Алгоритм використовується у великій кількості криптографічних застосунків.
Опис алгоритму:
Безпека алгоритму RSA побудована на принципі складності факторизації цілих чисел. Алгоритм використовує два ключі — відкритий (public) і секретний (private), разом відкритий і відповідний йому секретний ключі утворюють пари ключів (keypair). Відкритий ключ не потрібно зберігати в таємниці, він використовується для шифрування даних. Якщо повідомлення було зашифровано відкритим ключем, то розшифрувати його можна тільки відповідним секретним ключем.
Для того, щоб згенерувати пари ключів виконуються такі дії:
1. вибираються два великі прості числа 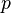 і
і 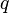 приблизно 512 біт завдовжки кожне
приблизно 512 біт завдовжки кожне
2. обчислюється їх добуток 
3. обчислюється функція Ейлера 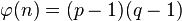
4. вибирається ціле  таке, що
таке, що  та
та  взаємно просте з
взаємно просте з 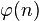
5. за допомогою розширеного алгоритму Евкліда знаходиться число 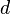 таке, що
таке, що 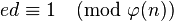
Число 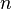 називається модулем, а числа
називається модулем, а числа  і
і 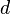 — відкритою й секретною експонентами відповідно. Пари чисел
— відкритою й секретною експонентами відповідно. Пари чисел 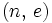 є відкритою частиною ключа, а
є відкритою частиною ключа, а 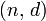 — секретною. Числа
— секретною. Числа 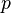 і
і 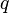 після генерації пари ключів можуть бути знищені, але в жодному разі не повинні бути розкриті.
після генерації пари ключів можуть бути знищені, але в жодному разі не повинні бути розкриті.
Для того, щоб зашифрувати повідомлення 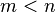 обчислюється
обчислюється
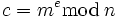 .
.
Число  використовується в якості шифротексту. Для розшифрування потрібно обчислити
використовується в якості шифротексту. Для розшифрування потрібно обчислити
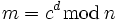 .
.
Неважко переконатися, що при розшифруванні ми відновимо вихідне повідомлення:
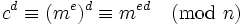
З умови
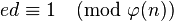
випливає, що
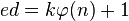 для деякого цілого
для деякого цілого 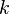 , отже
, отже
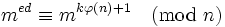
Згідно з теоремою Ейлера:
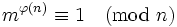 ,
,
тому
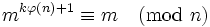
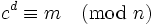
RSA працює значно повільніше симетричних алгоритмів. Для підвищення швидкості шифрування відкритий показник  вибирається невеликим, звичайно 3, 17 або 65537 (2 обрати не можна, бо
вибирається невеликим, звичайно 3, 17 або 65537 (2 обрати не можна, бо  повинно бути взаємно простим із
повинно бути взаємно простим із 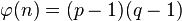 ). Ці числа у двійковому вигляді містять тільки по дві одиниці, що зменшує число необхідних операцій множення при піднесенні до степеня. Наприклад, для піднесення числа
). Ці числа у двійковому вигляді містять тільки по дві одиниці, що зменшує число необхідних операцій множення при піднесенні до степеня. Наприклад, для піднесення числа  до степеня 17 потрібно виконати тільки 5 операцій множення:
до степеня 17 потрібно виконати тільки 5 операцій множення:
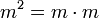
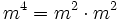
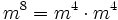

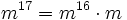
Вибір малого значення відкритого показника може призвести до розкриття повідомлення, якщо воно відправляється відразу декільком одержувачам, але ця проблема вирішується за рахунок доповнення повідомлень.
Значення секретного показника 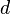 повинне бути досить великим. У 1990 році Міхаель Вінер показав, що якщо
повинне бути досить великим. У 1990 році Міхаель Вінер показав, що якщо 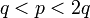 і
і 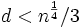 , то є ефективний спосіб обчислити
, то є ефективний спосіб обчислити 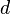 по
по 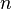 і
і  . Однак, якщо значення
. Однак, якщо значення  вибирається невеликим, то
вибирається невеликим, то 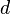 виявляється досить великим і проблеми не виникає.
виявляється досить великим і проблеми не виникає.
Система RSA використовується для захисту програмного забезпечення й у схемах цифрового підпису. Також вона використовується у відкритій системі шифрування PGP.
Через низьку швидкість шифрування (близько 30 кбіт/сек при 512 бітному ключі на процесорі 2 ГГц), повідомлення звичайно шифрують за допомогою продуктивніших симетричних алгоритмів з випадковим ключем (сеансовий ключ), а за допомогою RSA шифрують лише цей ключ.
Алгоритм електронного цифрового підпису Ель Гамаля (EGSA)
Надійний та зручний для реалізації на персональних комп’ютерах алгоритм цифрового підпису був розроблений у 1984 році американцем арабського походження Тахером Ель Гамалем. У 1991 році Національний інститут стандартів (НІСТ) США обґрунтував перед комісією Конгресу США вибір цього алгоритму як бази для відповідного національного стандарту. Найменування EGSA має походження від слів El Gamal Signature Algorithm
(алгоритм цифрового підпису Ель Гамаля). Ідея EGSA базується на тому, що для практичної неможливості фальсифікації ЕЦП може бути використана практично нерозв’язувана задача дискретного логарифмування.
Алгоритм
1. Перший користувач вибирає випадкове секретне число k, взаємно просте з Р-1, і обчислює число A^k mod P
2. Потім застосовуємо алгоритм Евкліда для значення b рівнянні:
m = (X1 * а +k * b) mod (P-1)
Пара чисел (а, b) буде цифровим підписом повідомлення m.
3. Повідомлення m разом з підписом (а, b) відправляється користувачеві 2.
4. Користувач 2 отримує повідомлення m і з використанням відкритого
ключа першого абонента Y1 обчислює два числа за наступними формулами
с1=Y1^a * a^b mod P, c2= A^m mod P
Якщо с1 = с2, то цифровий підпис першого користувача вірний.
Приклад обчислення і перевірки цифрового підпису
Маємо наступні загальні параметри: Р = 43, А = 23.
Один з користувачівпідписує своє повідомлення m=15 цифровим підписом, сформованим по алгоритму Ель Гамаля. Спочатку він обирає собі закритий ключ Х1=7 і формує відкритий
ключ: Y1 = 23^27 mod 41 = 4. Відкритий ключ передаємо іншим партнерам. Потім обираємо випадкове секретне число до, взаємно просте з Р-1. Нехай k=12. Далі обчислюємо число a = A^k mod P = 23^13 mod 41 = 31
Потім за допомоою алгоритму Евкліда знаходиться b в рівнянні:
m = (X1 * а +k * b) mod (P-1) = 15=7 * 31+13 * 6 mod 40
Рішенням буде значення b=6.
Таким чином, пара чисел (31, 6) буде цифровим підписом повідомлення m=15.
Потім інший партнер перевіряє цифровий підпис в повідомленні(за бажанням): він отримує отримує відкритий ключ першого користувача та обчислює с1 і с2 і порівнює їх.
с1=Y1^a * a^b mod P=23^7 * 31^6 mod 41=40,
c2= A^m mod P= 23^15 mod 41= 40
Якщо с1 = с2, то цифровий підпис в повідомленні m=15 вірний.
|
|
