Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Полные метрические пространства

Определение 6.1. Последовательность (x_n) метрического пространства (Х, r)называется фундаментальной, если (" e> 0)($N)(" n, m > N) Þ [ r (x_m, x_n) < e ].

Примером фундаментальной последовательности является любая сходящаяся последовательность точек метрического пространства.

В пространствеRлюбая фундаментальная последовательность сходящаяся. Но не всякая фундаментальная последовательность метрического пространства (Х, r)сходится в этом пространстве.

Например, в метрическом пространстве Х = (Q; r = ½ х- в ½) последовательность x_n = (1 + 1 /n) ⁿ ® e, если n ® ¥, но е Î I и eÏ X.

Определение 6.2. Метрическое пространство называется полным метрическим пространством, если любая фундаментальная последовательность точек этого пространства сходится в нем.

Пример 6.1. Метрическое пространство R – полное метрическое пространство, поскольку любая его фундаментальная последовательность сходится к числу, которое принадлежит пространству R. Это следует из критерия Коши: для того, чтобы числовая последовательность была сходящейся, необходимо и достаточно, чтобы она была фундаментальной.

Пример 6.2. Докажем, что пространство R^m - полное метрическое пространство.

3Пусть последовательность(x _n= (x ₁⁽ⁿ⁾, x ₂⁽ⁿ⁾, …, x _m⁽ⁿ⁾)) (6.1) – произвольная функциональная последовательность пространства R^m. Покажем, что последовательность сходящаяся и ее предел принадлежит пространству R^m.

По определению фундаментальной последовательности и определению метрики в пространстве R^m

(" e> 0)($ N (e))(" p, n > N) Þ [ r (x_p, x_n) < e ] Þ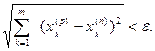

Согласно доказательству теоремы 5.1 ½ x_k^(p) - x_k⁽ⁿ⁾ ½ < e. Таким образом, доказана фундаментальность числовых последовательностей (x₁⁽ⁿ⁾), (x₂⁽ⁿ⁾), …, (x_m⁽ⁿ⁾), а отсюда и их сходимость.

Пусть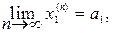

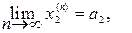
Рассмотрим точку а = (а₁, а₂, …, а_m). Поскольку а₁, а₂, …, а_mÎ R^m, то аÎ R^m. По теореме о покоординатной сходимости последовательности в пространстве (Х, r)получили, что в метрическом пространстве R^m последовательность (x_n) сходится к аÎ R^m Это значит, что пространство R^m полное метрическое пространство. 4

Пример 6.3. Докажем, что метрическое пространство С [ a, b ] является полным.

3Пусть (x_n) – произвольная фундаментальная последовательность в метрическом пространстве С [ a, b ]. Элементы ее непрерывные на [ a, b ] функции.

Докажем, что последовательность (x_n) сходится в метрическом пространстве С [ a, b ]. Спачатку докажем, что она сходится к предельной функции х (t) на отрезке [ a, b ].

По определению фундаментальной последовательности

(" e> 0)($N (e))(" m, n > N) Þ [ r (x_m, x_n) < e ] Þ

Þ ½ x_m (t)- x_n (t)½ < e " n, m > N Ù " tÎ [ a, b ] (6.2)

Это значит, что " tÎ [ a, b ] фундаментальной является функциональная последовательность (x_n). Поэтому она имеет предел.

Если в неравенстве (6.2) перейти к пределу при m®¥, то 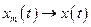. Получим

½ x (t)- x_n (t)½ £ e " n> N Ù " tÎ [ a, b ].

Таким образом, мы доказали, что

(" e> 0)($N (e))(" n > N Ù " tÎ [ a, b ]) Þ [½ x (t)- x_n (t)½ £ e ].

А это значит, что последовательность (x_n) равномерно сходится к функции х (t) на [ a, b ]. Поскольку все элементы функциональной последовательности (x_n) непрерывные на [ a, b ]функции, то предельная функция х (t) также непрерывна на этом отрезке и поэтому является элементом метрического пространства С [ a, b ]. По теореме 5.2 в этом пространстве последовательность (x_n) сходится к х (t). Это свидетельствует о полноте метрического пространства С [ a, b ]. 4