Теоремы об открытых и замкнутых множествах

Теорема 3.1. Объединение любого числа открытых множеств – множество открытое.

Пусть G_k, где k Î N - открытые множества.

Докажем, что - открытое множество.

3Выберем любую точку х _о Î G. По определению объединения множеств точка х _о принадлежит одному из множеств G_k. Поскольку G_k – открытое множество, то существует e - окрестность точки х_о, которая целиком лежит в множестве G_k: U (x_o, e) Ì G_k Þ U (x_o, e) Ì G.

Получили, что любаю точка х_оÎ G – внутренняя, а это значит, что G – открытое множество. 4

Теорема 3.2. Пересечение конечного числа открытых непустых множеств– множества открытое.

Пусть G_k (k = 1, 2, …, n) – открытые множества.

Докажем, что 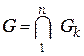- открытое множество.

3Выберем любую точку х _о Î G. По определению пересечения множеств х _о принадлежит каждому из множеств G_k. Поскольку каждое множество G_k открытое, то в любом множестве G_k существует e_k - окрестность точки х _о: U (x _o, e _k) Ì G_k. Множество чисел{ e ₁, e ₂, …, e_n } конечное, поэтому существует число e = min { e ₁, e ₂, …, e_n }. Тогда e - окрестность точки х _онаходится в каждой e_k - окрестности точки х _о: U (x _o, e) Ì U_e (x _o, e_k) Þ U (x _o, e) Ì G.

Получили, что х _о – внутренняя точка множества G, а это значит, что G – открытое множество. 4

Замечание 3.1. Пересечение бесконечного множества открытых множеств может и не быть открытым множеством.

Пример 3.1. Пусть в пространстве R G_k = (2 – 1 /k; 4 + 1 /k), где k= 1, 2, …, n, …. G₁= (1; 5), G₂ (1, 5; 4, 5), 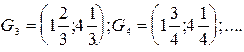Отрезок [2; 4] Ì G_k и не является открытым множеством, точки 2 и 4 не являются внутренними.

Теорема 3.3. Пересечение любой совокупности замкнутых непустых множеств – замкнутое множество.

Пусть F_k - замкнутые множества.

Докажем, что множество 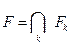замкнутое, т.е. оно содержит все свои предельные точки.

3Пусть х _о – предельная точка множества F. Из определения пересечения множеств следует, что в любой e - окрестности точки х _о находится бесконечно много точек каждого из множеств F_k, а это значит, что х _о – предельная точка каждого множества F_k. В силу замкнутости множеств F_k точка

х _о Î F_k " k Þ х _о Î F. Поскольку точка х _о выбрана произвольно, то все предельные точки принадлежат множеству F, а это значит множесто F замкнутое. 4

Теорема 3.4. Объединение конечного числа замкнутых множеств – множество замкнутое.

Пусть каждое множество F_k замкнутое.

Докажем, что множество замкнутое, т.е., если х _о – предельная точка множества F, то х _о Î F.

3Пусть х _о – любая предельная точка множества F, тогда в любой e - окрестности точки х _о существует бесконечно много точек множества . Поскольку количество множеств F_k конечное, то х _о принадлежит хотя бы одному из множеств F_k, т.е. х _о – предельная точка для этого множества.

В силу замкнутости F_k точка х _о принадлежит F_k, а поэтому и множеству . Поскольку точка х _о выбрана произвольно, то все предельные точки принадлежат множеству F, а это значит множество F замкнутое. 4

Замечание 3.2. Объединение бесконечного числа замкнутых множеств может быть множеством открытым.

Пример 3.2. В пространстве R: F_k = [2 + 1 /k; 5–1 /k ]

F₁ = [3; 4]; F₂ = [2, 5; 4, 5]; …. 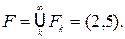Интервал (2; 5) – открытое множество.

Примем без доказательства теоремы 3.5 и 3.6, связанные с дополнением множества Е до множества Х: С_хЕ=СЕ.

Теорема 3.5. Если множество Е замкнутое, то его дополнение СЕ открытое множество.

Пример 3.3. Е= [2, 5], C_R E = (- ¥, 2) È (5, +¥).

Теорема 3.6. Если множество Е открытое, то его дополнение СЕ замкнутое множество.

Пример 3.4. Е= (2, 5), C_R E = (- ¥, 2] È [ 5, + ¥).