Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Предел и непрерывность отображений метрических пространств

Под отображением метрических пространств будем понимать отображение множеств элементов рассматриваемых метрических пространств. В дальнейшем метрическое пространство и множество его элементов будем обозначать одной буквой X или Y, а метрику соответственно r_X и r_Y.

Пусть f – отображение из метрического пространства X в метрическое пространство Y, т.е. f: с Х 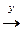Y, точка АÎ Y, x₀ – предельная точка D (f) (D (f) – область определения отображения f в пространстве Х).

Определение 7.1 ( по Гейне). Точка А называется пределом отображения f в точке х₀, если для любой последовательности (x_n), сходящейся к х_o по метрике r_х, с элементами, принадлежащими D (f) и отличными от х_о, соответствующая последовательность (f (x_n))сходится к А по метрике r_y.

Определение 7.2 (по Коши). Точка А называется пределом отображения f в точке х_о, если для любого положительного числа e существует положительное число d такое, что для всех точек х, принадлежащих D (f) и удовлетворяющих условию 0 < r_x (x, x_o) < d, выполняется неравенство r_Y (f (x), A) < e.

Если точка А является пределом отображения f в точке х_о, то пишут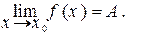

Сформулированные выше определения символично записывают следующим образом.

Определение 7.1*.

Û " (x_n) |x_n x_o, x_nÎ D (f), x_n¹ x_o Þ f (x_n) 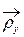A.

Определение 7.2*.

(" e> 0)($d (e) > 0)(" xÎ D (f) | 0 < r_X (x, x_o)< d) Þ [ r_Y (f (x), A) < e ].

Примеры определения 7.2 в различных метрических пространствах.

7.1. Пространство R²: X = R, Y = R; f: с 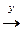R R.

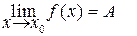Û (" e > 0)($d (e)> 0)(" x Î D (f)ç 0< r_X (x, x_o < d)Þ [ r_Y (f (x), A) < e ].

7.2. Пространство R³: X = R², Y = R, f: с R² 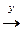R, x= (x₁, x₂), x_o= (x₁^o, x₂^o), x®x_o Û Û x₁®x₁^o Ù x₂ ®x₂^o.

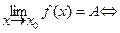
Û (" e> 0)($d (e) > 0)(" xÎ D (f)ç 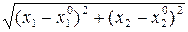< d) Þ [ r_Y (f (x), A) < e ].

Теорема 7.1. Определения 1 и 2 равносильны.

С доказательством можно ознакомиться в [1, стр.22-23].

Определение 7.3. Пусть f – отображение из метрического пространства X в метрическое пространство В (f: с Х 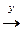Y), точка х_оÎ D (f). Отображение f называется непрерывным в точке х_о, если

(" e> 0)($d (e) > 0)(" xÎ D (f) | r_X (x, x_o) < d)) Þ [ r_Y (f (x), f (x_о)) < e ].

Замечание 7.1. В этом определении не требуется, чтобы точка х_о была предельной точкой D (f). Она может быть как предельной, так и изолированной точкой.

Определение 7.3 *. Если точка х_о – предельная точка D (f), то отображение f непрерывное в точке х_о тогда и только тогда, когда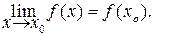

Если точка х_о – изолированная точка D (f), то отображение f всегда непрерывно в точке х_о.

Определение 7.4. Отображение f: Х 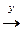Y называется непрерывным на множестве Х, если оно непрерывно в каждой точке этого множества.

Теорема 7.2. Отображение f: Х 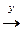Y является непрерывным тогда и только тогда, когда при этом отображении прообраз каждого открытого (замкнутого) в В множества является множеством, открытым (замкнутым) в Х. Это значит, что если множество GÌ Y – открытое (замкнутое) множество, то множество f ^-1 (G) – открытое (замкнутое) в Х.

С доказательством можно ознакомится в [1, cтр.24-25]

Определение 7.5. Отображение f: с Х 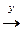Y называется равномерно непрерывным на множестве ЕÌ Х, если

(" e> 0)($d> 0)(" x₁, х₂Î Е | r_X (x₁, x₂) < d) Þ [ r_Y (f (x₁), f (x₂)) < e ].

Замечание 7.2. Если отображение f: Х 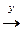Y равномерно непрерывноена множестве ЕÌ Х, то оно и непрерывное на Е. Обратное утверждение не имеет места.

Определение 7.6. Метрическое пространство Х называется связным, если его нельзя представить в виде объединения двух непустых открытых (замкнутых) множеств.

Определение 7.7. Множество ЕÌ Х называется связным в метрическом пространства Х, если связным является подпространство Е метрического пространства Х.

Определение 7.7*. Множество ЕÌ Х называется связным, если любые две точки этого множества можно соединить ломаной, которая целиком лежит в этом множестве.

Примеры: 1) в пространства R связными являются интервал, отрезок, луч, множество {3};

2) в пространстве R² – круг, кольцо;

3) множество Е = (0, 1) È [3, 4] Ì R не является связным множеством.

Теорема 7.3. При непрерывном отображении образом связного множества является связное множество.

3от противного.

Пусть множество f (X) не является связным в метрическом пространстве Y. Тогда существуют два непустых, непересекающихся между собой, открытых множеств М и N таких, что f (X) = MÈ N.

По теореме 2 в силу непрерывности отображения f прообразы множеств М и N (f ^{- 1}(M)и f ^{- 1}(N)) будут открытыми. Очевидно, что они будут также непустыми, непересекающимися между собой множествами, а их объединение есть множество Х. Итак, множество Х есть объединениедвух непустых, непересекающихся, открытых множеств, это противоречит связности множества Х. 4