
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Полином Ньютона. Метод конечных разностей
|
|
Полином Лагранжа, как правило, применяется для вычисления значения функции в точке, лежащей внутри интервала, содержащего узловые точки, но не совпадающей ни с одной узловой точкой. Для таких вычислений не обязательно иметь общий вид функции  . Для получения общего вида интерполяционного полинома (а затем и многочлена) чаще применяют полином Ньютона. Он может быть получен из полинома Лагранжа и, соответственно, является одним из его частных следствий. Полином Ньютона имеет вид:
. Для получения общего вида интерполяционного полинома (а затем и многочлена) чаще применяют полином Ньютона. Он может быть получен из полинома Лагранжа и, соответственно, является одним из его частных следствий. Полином Ньютона имеет вид:
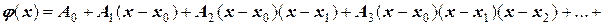
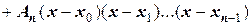 .
.
Значения коэффициентов Аi можно получить, если последовательно подставлять в уравнение полинома значения переменных хi → x0, x1, x2, …, xn. Требование совпадения значения полинома с заданными значениями функции в узловых точках приводит к системе линейных уравнений:
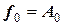 при
при 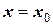 ;
;
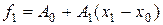 при
при 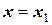 ;
;
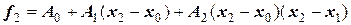 при
при 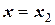 ;
;
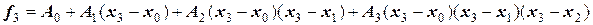
при 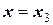 ;
;
……………………………………………………………………….
Из этих уравнений легко находятся коэффициенты Аi:
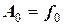 ;
;
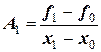 ;
;
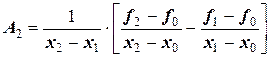 и т.д.
и т.д.
Безусловно, вычисление коэффициентов становится весьма трудоемкой операцией. Однако существует более удобный и компактный способ нахождения коэффициентов полинома Ньютона. Но первоначально решим представленную выше задачу, воспользовавшись полиномом Ньютона.
Задача 18. Произвести интерполяцию таблично заданной функции полиномом Ньютона.
| х | 0, 5 | 1, 0 | 1, 5 | 2, 0 |
| f | 2, 75 | 4, 0 | 8, 75 |
Решение. Воспользовавшись вышеприведенными соотношениями для вычисления коэффициентов полинома Ньютона, определим:
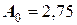 ;
; 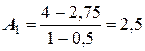 .
.
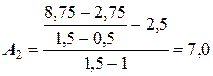 .
.
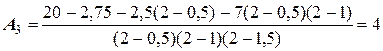 .
.
Следовательно, полином Ньютона примет вид:
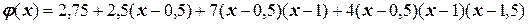 .
.
Если выполнить необходимые арифметические действия и привести подобные члены, получим окончательно интерполяционную функцию:
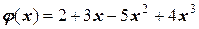 .
.
Получив решение вышеприведенной задачи, попробуем найти коэффициенты полинома Ньютона следующим образом. Применительно к функции 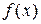 выполним некоторые расчеты, результаты которых занесем в следующую таблицу.
выполним некоторые расчеты, результаты которых занесем в следующую таблицу.
Таблица 19 - Рачет коэффициентов полинома Ньютона
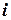
| 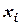
| 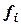
| 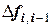
| 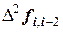
| 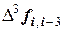
|
| 0, 5 1, 0 1, 5 2, 0 | 2, 75 4, 0 8, 75 20, 0 | 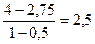
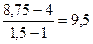
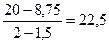
| 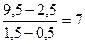
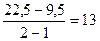
| 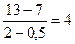
|
В столбце 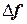 записаны частные от деления
записаны частные от деления
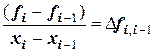 .
.
В столбце 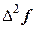 записаны частные от деления
записаны частные от деления
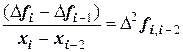 .
.
Соответственно в столбце 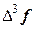 записаны частные от деления
записаны частные от деления
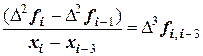 ,
,
где индекс i=1…n.
Заметим, что в таблице в первой строке имеем следующий ряд чисел: 2, 75; 2, 5; 7, 0; 4, 0. Это коэффициенты в ранее полученном полиноме Ньютона и начальная граница интервала. Очевидно, что табличный расчет существенно облегчил получение коэффициентов Ai в полиноме Ньютона. Таблица 19, представленная выше, называется таблицей конечных разностей. Величины 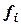 называются конечными разностями нулевого порядка,
называются конечными разностями нулевого порядка, 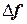 - конечные разности первого порядка,
- конечные разности первого порядка, 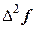 - конечные разности второго порядка и т.д. до
- конечные разности второго порядка и т.д. до 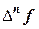 - конечная разность п – го порядка.
- конечная разность п – го порядка.
Примечание: термин “конечные разности” применяется в случае разбиения отрезка интерполирования на равные интервалы. Если разбиение неравномерное, то применяется термин “разделенные разности”.
В задаче 18 интерполяция проводилась на всем отрезке задания функции [ x0 ; x3 ] с интервалом 0, 5. Однако с помощью таблицы конечных разностей очень легко построить интерполяционный полином на любом интервале (в пределах заданного отрезка) и, что иногда важно, взять за основу любую границу (не обязательно ею должна быть а=х0). Например, нам интересна интерполяция на отрезке [ x0 ; x1 ] Тогда полином Ньютона примет следующий вид:
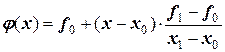
или
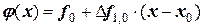 .
.
Построим геометрический образ этого полинома первой степени (рисунок 17).
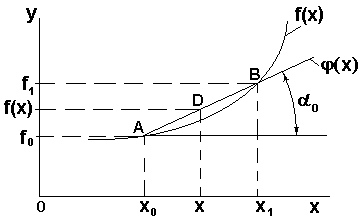
Рисунок 17 - Геометрическая трактовка конечной разности
Очевидно, что функции  будут соответствовать все точки отрезка АВ (например, точка D). Тогда, если, например, х=х1, получим
будут соответствовать все точки отрезка АВ (например, точка D). Тогда, если, например, х=х1, получим
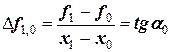 .
.
Можно утверждать, что
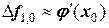 .
.
Иначе, конечные разности первого порядка – это приближенные значения первых производных заданной функции в начале интервала. Точно так же можно показать, что остальные конечные разности – суть производные соответствующего порядка, взятые на границе соответствующего интервала. Например, 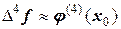 . Эти выводы крайне важны и в другом аспекте – с помощью построения таблицы конечных разностей можно производить численное дифференцирование любой (в том числе и заданной аналитически) функции.
. Эти выводы крайне важны и в другом аспекте – с помощью построения таблицы конечных разностей можно производить численное дифференцирование любой (в том числе и заданной аналитически) функции.
Вполне понятно, что интерполяционный график функции по двум точкам [ x0 ; x1 ] – это прямая линия, уравнение которой мы и получили. Это так называемая линейная интерполяция. Нетрудно также видеть, что, если (х1 –х0) → 0, то
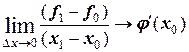 .
.
В качестве примера можно записать полином Ньютона при интерполяции вышерассмотренной функции на участке [ x1=1, 0; x2=2, 0 ]. Он будет иметь вид:
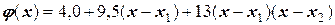
или 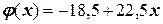 .
.
Полином Ньютона, а также расчет конечных разностей, упрощается, если табличная функция представлена на отрезке с равноотстоящими интервалами, т.е.
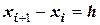 .
.
Тогда коэффициент Ат в полиноме Ньютона (если за начало отрезка интерполирования принять х0) надо вычислять по формуле:
 ,
,
а конечные разности рассчитываются так, как показано в таблице 20.
Таблица 20 - Запись конечных разностей
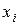
| 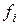
| 
| 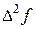
| 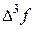
|
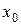
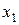
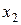
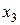
| 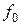
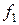
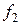
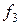
| 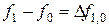
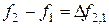
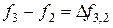
| 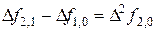
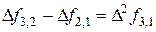
| 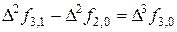
|
Полином Ньютона записывается следующим образом:
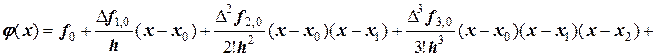
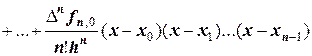 .
.
В таком виде полином Ньютона называют первым интерполяционным многочленом Ньютона.
|
|