Приближение функции методом наименьших квадратов

Выше рассматривалась интерполяция, т.е. такой способ аппроксимации, когда значения исходной и аппроксимирующей функций совпадают в узлах некоторой сетки. Однако достаточно часто, например, при аппроксимации большого числа экспериментальных точек, найденных с некоторой погрешностью, интерполяция становится неразумной. Такая же проблема возникает при обработке данных экспериментов, когда на функциональный отклик могут влиять случайные неконтролируемые независимые факторы, искажающие полезную информацию. В этом случае целесообразно строить аппроксимирующую функцию таким образом, чтобы сгладить влияние погрешности измерения как вызывающие незначительные отклонения в результате действия «шума» и т.п. Такое сглаживание обычно называют “приближением”. При этом возникает две проблемы.

Первая связана с тем, что тип и общий вид заменяющей функции всегда заранее определяет экспериментатор. Его выбор базируется на чисто визуальной оценке расположения экспериментальных (табличных) точек в пределах выбранной координатной системы (если это возможно). Безусловно, решение в этом случае будет в значительной степени зависеть от опыта и профессионализма экспериментатора. Для определенности и простоты мы будем в дальнейшем рассматривать наиболее часто встречающийся случай, когда аппроксимирующая функция является многочленом.

Вторая проблема приближения заключается в следующем. Пусть даны результаты наблюдений, представленные в табличной форме (см. таблицу 17). Представим эту таблицу графически, где в координатной системе xof представлено несколько начальных точек, например, А₀, В₀, С₀, рисунок 19 _.. Функцию f(x) аппроксимируем функцией y=φ (х) таким образом, чтобы ее график «усредненно» проходил в области экспериментальных точек, «сглаживая» действие случайных факторов.

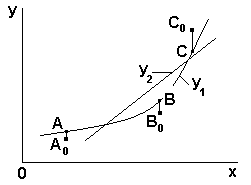
Рисунок 19 - К усреднению табличной функции

Так как снято требование обязательного прохождения графика аппроксимирующей функции через экспериментальные точки, таких графиков можно провести бесчисленное множество. Для получения однозначности надо ввести дополнительное требование – требование оптимальности:

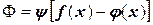→ min.

Существует несколько критериев такой опатимальности. Наиболее часто и успешно при построении приближающей функции применяют метод наименьших квадратов. Он предполагает нахождение такой аппроксимирующей функции φ (х) по отношению к значениям f(x), для которой минимальной будет сумма квадратов отклонений между этими функциями в экспериментальных точках, т.е.

→ min.

Графически это означает, что кривая функции φ (х) должна так пройти в области точек f(x), чтобы соблюдалось условие:

.

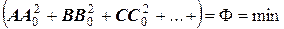Будем искать функцию φ (х) в виде многочлена:

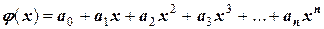
или .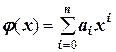

Найти функцию φ (х) – это значит подобрать такие числовые значения а₀, а₁, …, а_п, при которых выполнялось бы условие минимизации функции Ф:

,

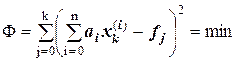где k – количество экспериментальных точек.

Очевидно, мы имеем (п+1) неизвестное и, соответственно, надо иметь не меньше уравнений для их нахождения. Рассмотрим случай, когда k=n.

Условие минимизации функции Ф можно записать следующим образом:

,

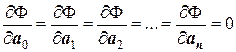то есть равенство нулю первых частных производных функции Ф по неизвестным (а₀, а₁, …, а_п). Рассмотрим случай, когда задано всего три экспериментальные точки, т.е. п=2. Этого достаточно, чтобы обобщить результаты на любое количество точек. Пусть имеются результаты наблюдения:

для которых будем искать аппроксимирующий многочлен 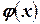второй степени. Предположим, он найден. Тогда можно расчетом найти:

.

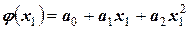
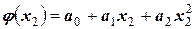Соответственно, можно рассчитать и отклонения между 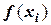и :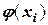

,

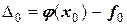
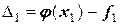
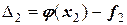а затем и значение функции Ф:

.

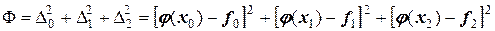Взяв частные производные по коэффициентам а_i и сгруппировав подобные члены в каждом из уравнений, получим их в следующем виде:

.

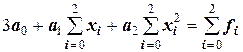
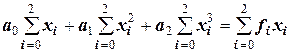
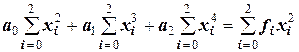Таким образом, получили систему из трех линейных уравнений с неизвестными (а₀, а₁, а₂), которая имеет вид в векторной форме:

,

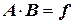где ,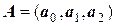

, .

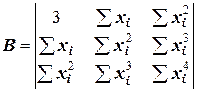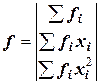Анализ структуры векторов А, В, f показывает, что аппроксимирующий функцию f(x) многочлен п -ой степени при (п+1) узловых точках будет описываться векторным уравнением системы линейных уравнений:

,

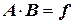где ,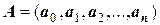

, .

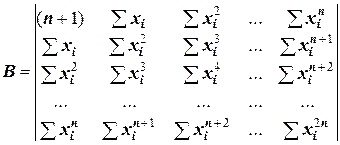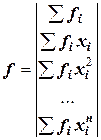Заметим, что матрица коэффициентов В симметрична относительно диагонали, поэтому транспонирование эту матрицу не изменяет. Это обстоятельство и вид других векторов, весьма простых, делает процедуру записи этих векторов для функции, заданной количеством точек N и аппроксимируемой многочленом п -ой степени, очевидной и простой. Например, запишем вектора A, B, f для четырех экспериментальных точек, на основе которых можно получить многочлен третьей степени:

,

, .

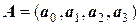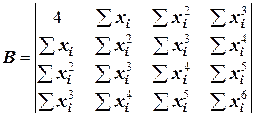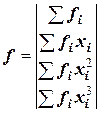Для практической реализации системы линейных уравнений и нахождения затем аппроксимирующего многочлена по результатам экспериментальных наблюдений составляют расчетную таблицу, которая, например, для четырех точек принимает следующий вид (таблица 21).

Таблица 21 - Расчетная таблица метода наименьших квадратов

i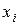

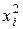
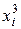
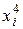
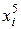
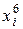
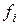
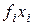
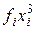
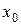
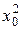
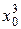
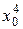
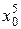
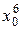
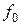
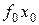
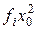
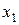
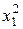
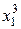
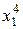
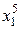
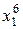
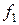
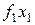
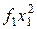
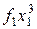
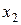
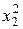
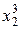
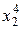
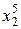
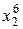
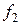
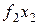
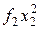
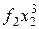
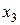
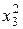
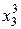
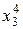
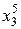
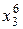
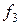
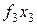
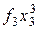
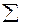
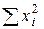
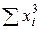
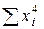
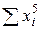
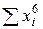
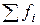
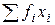
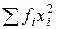
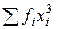
Наиболее часто методом наименьших квадратов проводят линейную, квадратическую и (реже) кубическую аппроксимацию. На основании общего вида векторной записи системы линейных уравнений коэффициенты соответствующих многочленов можно определить по векторам.

а) Линейная аппроксимация. Задача заключается в определении коэффициентов многочлена 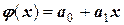из системы уравнений ,

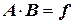где ,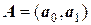

, .

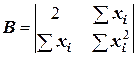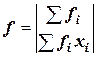Коэффициенты находят по формулам Крамера:

, .

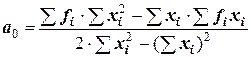б) Квадратическая аппроксимация. Задача заключается в определении коэффициентов многочлена .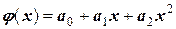

Они рассчитываются как неизвестные из системы трех линейных уравнений, векторно описанных выше. Корни этой системы (коэффициенты) также могут быть определены по формулам Крамера.

в) Кубическая аппроксимация. Задача заключается в определении коэффициентов многочлена

.

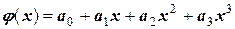Как и в предыдущих случаях, они рассчитываются как неизвестные, но уже системы четырех линейных уравнений, также векторно описанных выше. Но корни этой системы целесообразно находить, пользуясь описанными выше методами решения линейных уравнений (например, методом Гаусса).

Аппроксимация табличной функции многочленом методом наименьших квадратов с увеличением степени многочлена быстро теряет точность в связи с очевидной периодичностью многочлена (смотри раздел о точности полиномиальной интерполяции функции). Поэтому в практике аппроксимация по описанной схеме выше кубической не применяется.

Аппроксимация методом наименьших квадратов широко применяется в математической статистике для нахождения уравнений регрессии, т.е. уравнений, с помощью которых функционально устанавливается связь между независимыми (х_i) и зависимыми (f_i) параметрами (факторами) при статистическом разбросе последних. При этом экспериментатор, как правило, располагает значительным набором пар (x_i, f_i), превышающим две или три пары (необходимые, например, для линейной или квадратической аппроксимации). Схема расчетов коэффициентов 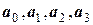при этом не меняется.

Задача 19. Результаты экспериментальных наблюдений представлены в таблице 22. Произвести линейную и квадратическую аппроксимацию методом наименьших квадратов. Определить остаточное квадратическое отклонение. Сравнить их по двум способам аппроксимации.

Таблица 22 - Расчетная таблица к задаче 19

i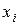
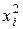
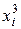
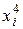
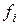
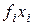
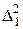
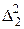
					2, 2	2, 2	2, 2	0, 8836	0, 0713
					3, 0	3, 0	3, 0	3, 0276	0, 2840
					5, 0			3, 8612	1, 8530
					6, 5			0, 2162	0, 0192
								0, 4489	0, 2887
								0, 1089	2, 3635
								5, 6402	3, 1368
								0, 1406	0, 0524
								0, 8464	0, 0822
								3, 6814	0, 5087
					126, 7	494, 2	2095, 2	18, 8550	8, 6598

Решение. Из характера представленных в таблице данных видно, что наблюдения были выполнены при пяти уровнях изменения независимого фактора х путем повторных измерений. Таким образом имеем 10 пар наблюдений. Принцип параллельности (повторения) опытов применяется весьма часто для компенсации элементов случайности, имеющих место в реальных исследованиях.

Система линейных уравнений будет иметь вид:

а) для линейной аппроксимации

,

, , ;

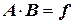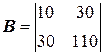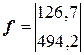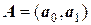б) для квадратической аппроксимации

,

, , .

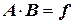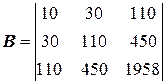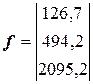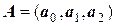Решения этих систем методом Крамера дают следующие результаты:

а) уравнение линейной аппроксимации

;

б) уравнение квадратической аппроксимации

.

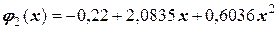В таблице также приведены квадратичные остаточные разности

,

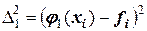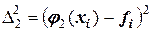
и их сумма. Видно, что суммарная остаточная разность для квадратической аппроксимации более чем в два раза меньше, т.е. эта аппроксимация ближе к экспериментальным данным. В математической статистике величина

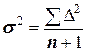
называется дисперсией, а величина

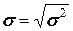
называется среднеквадратическим отклонением. По физической природе дисперсия и среднеквадратическое отклонение различны так же, как, например, длина и площадь, или говорят, что эти величины имеют разную размерность. Безусловно, только среднеквадратическое отклонение имеет размерность функции. В вышеприведенном примере эти характеристики соответственно равны:

а) для линейной аппроксимации

,

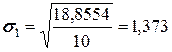б) для квадратической аппроксимации

.

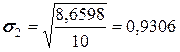Видно, что при квадратической аппроксимации среднеквадратическое отклонение существенно ниже.