
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Прямой метод исключения Гаусса
|
|
Прямые методы основаны на принципах последовательного исключения неизвестных. Целью исключения является преобразование базовой матрицы системы А из размерности 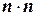 в другую размерность. Наиболее просто решается система линейных уравнений с n -неизвестными в том случае, когда штатная матрица
в другую размерность. Наиболее просто решается система линейных уравнений с n -неизвестными в том случае, когда штатная матрица 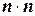 преобразуется в диагональную матрицу:
преобразуется в диагональную матрицу:
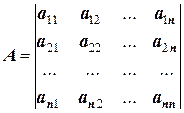 =
= 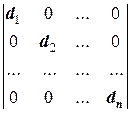 ;
; 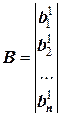
Тогда первичная система из n линейных уравнений, каждое из которых содержит (теоретически) (n) неизвестных, распадается на n линейных уравнений, каждое из которых содержит только одну неизвестную величину типа
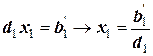 ;
;
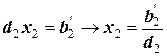 ;
;
…………………..
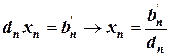 .
.
В таком случае основная вычислительная работа будет заключаться в преобразовании исходной системы линейных уравнений. Это трудоемкая процедура. Более проста схема преобразования матрицы размерностью 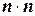 в треугольную. Такого типа матриц может быть два вида, в зависимости от условия
в треугольную. Такого типа матриц может быть два вида, в зависимости от условия 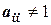 или
или 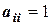 . Первая имеет вид:
. Первая имеет вид:
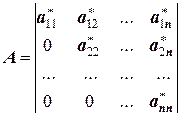 ;
; 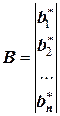
Тогда из последнего уравнения в одно действие определяется значение неизвестной 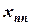 :
:
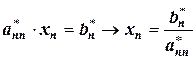 .
.
Из предпоследнего уравнения получим:
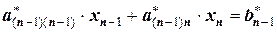 ,
,
а затем 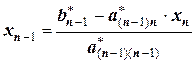
И так далее, вплоть до первого уравнения:
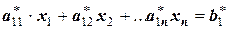 ;
;
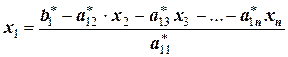 .
.
Преобразование квадратной матрицы в треугольную можно выполнить, воспользовавшись одним из свойств определителя: если одну из строк (или столбцов) умножить на любое число и сложить (вычесть) с другой строкой, то от этого определитель не изменится. Например, умножив вторую строку на коэффициент k1, а третью – на коэффициент k2 и порознь сложив их с первой, получим эквивалентную матрицу:
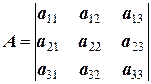
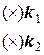 =
= 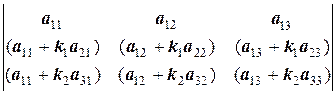 .
.
Коэффициенты всегда можно подобрать так, чтобы нужный элемент матрицы принял нужную нам величину (в том числе и ноль, что в методе Гаусса и требуется). Последовательно осуществляя этот процесс, можно получить треугольную матрицу.
Метод Гаусса (метод последовательного исключения неизвестных) включает в себя две процедуры: прямой ход и обратный ход. Прямой ход - приведение квадратной матрицы, например, к верхней треугольной форме, обратный ход - нахождение неизвестной в направлении от 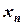 к
к 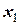 (см. выше), что эквивалентно приведению матрицы к диагональной форме. Рассмотрим этот метод на наиболее простой системе, состоящей из трех линейных уравнений:
(см. выше), что эквивалентно приведению матрицы к диагональной форме. Рассмотрим этот метод на наиболее простой системе, состоящей из трех линейных уравнений:
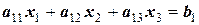
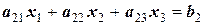
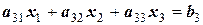 .
.
Систему можно записать в векторной форме:
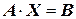 ,
,
где
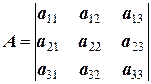 ,
, 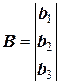 ,
, 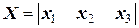 .
.
По методу Гаусса умножим вторую строку на коэффициент  и вторую строку запишем в виде суммы первой и второй, третью строку умножим на коэффициент
и вторую строку запишем в виде суммы первой и второй, третью строку умножим на коэффициент 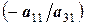 и также сложим с первой.
и также сложим с первой.
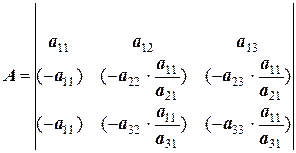 ;
; 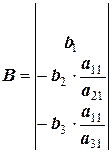 ;
;
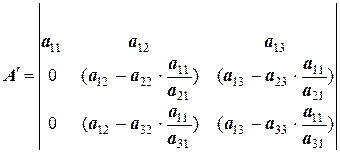 ;
; 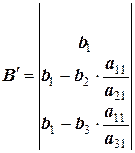
или
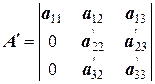 ;
; 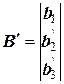 ,
,
где 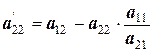 ;
; 
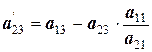
 ;
;
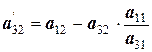 ;
; 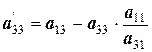 ;
;
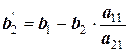 ;
; 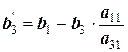 .
.
Так же поступим и с матрицей А ’: умножим третью строку на коэффициент 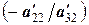 , сложим вторую и третью строки, записав результат в третью строку:
, сложим вторую и третью строки, записав результат в третью строку:
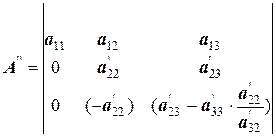 ;
; 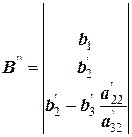
Получим треугольную матрицу А ’’
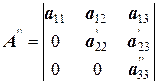 ;
; 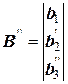 ,
,
где 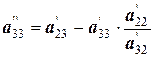 ;
;  .
.
Видим, что процесс реконструкции исходной матрицы носит пошаговый характер и с каждым шагом мы получаем промежуточную матрицу, порядок которой на единицу меньше предыдущей. Тогда исходная система линейных уравнений примет следующую структуру:
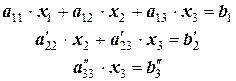
После преобразования системы следует обратный ход. Он заключается в последовательном вычислении переменных в направлении снизу вверх. Например:
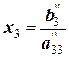 ;
; 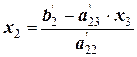 ;
; 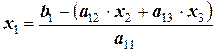 .
.
Задача 13. Решить систему линейных уравнений, найти корни с точностью до 0, 001.
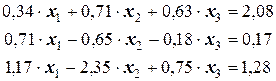 .
.
Решение. Всю систему расчетов, как правило, пошагово представляют в табличной
форме. Она может быть разной. Например, такой, как представлено в таблице 11, где все решение представляется в виде двухшагового цикла.
Таблица 11 - Расчетная таблица системы линейных уравнений
| Шаг | Элементы матрицы | Свободные члены | Множитель |
| 0, 34 0, 71 0, 63 0, 71 -0, 65 -0, 18 1, 17 -2, 35 0, 75 | 2, 08 0, 17 1, 28 | -0, 34/0, 71= - 0, 4789 -0, 34/1, 17= - 0, 2906 | |
| 0, 34 0, 71 0, 63 | 2, 08 | -1, 0212/1, 3929= - 0, 7331 | |
| 0 1, 0212 0, 7162 0 1, 3929 0, 4120 | 1, 9985 1, 7080 | ||
| 0 1, 0212 0, 7162 | 1, 9985 | ||
| 0 0 0, 4141 | 0, 7463 |
Получили систему из трех уравнений (они выделены в таблице в отдельные строки:
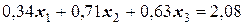 ;
;
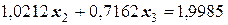 ;
;
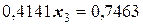 .
.
Далее, методом обратного хода, найдем неизвестные:
 ;
; 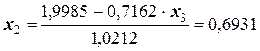
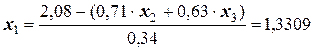 .
.
При первом шаге коэффициенты при неизвестных во втором и третьем уравнениях получены путем их умножения на соответствующий множитель и сложения по столбцам с коэффициентами первого уравнения.
Рассмотрим еще одну, более удобную расчетную схему, которая называется схемой единственного деления. Ее смысл очевиден из анализа таблицы 12.
Целью преобразований является получение верхней треугольной матрицы, в диагонали которой стоят единицы. Для этого в текущей матрице первое уравнение должно быть разделено на значение первого элемента, а уже преобразованная строка, умноженная на первые элементы (с обратным знаком) других строк, складывается с этими строками. В результате исходная система уравнений преобразуется к
Таблица 12 - Решение системы уравнений по схеме единственного деления
| Шаг | Элементы матрицы | Свободный коэф. | Множитель |
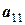 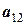 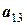
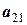 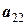 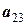
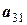 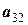 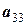
| 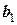
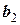
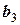
| 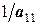
| |
 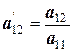 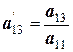
| 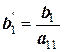
| 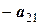 ; ; 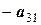
| |
0 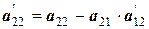 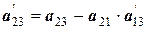 0
0 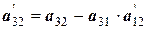 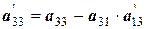
| 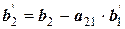
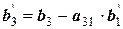
| 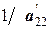
| |
0 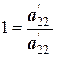 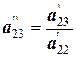
| 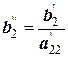
| 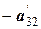
| |
0 0 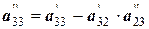
| 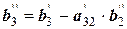
| 
| |
| 0 0 1 | 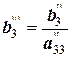
|
следующему виду:
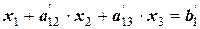
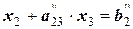
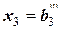 .
.
Методом обратного хода получаем:
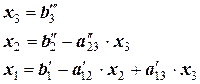 .
.
Найдем корни ранее рассмотренного уравнения, используя схему единственного деления (таблица 13).
Таким образом, исходная система принимает вид:
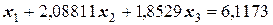 ,
,
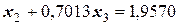 ,
,
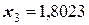 .
.
Таблица 13 - Решение задачи 13 по схеме единственного деления
| Шаг | Элемент матрицы | Свободный коэффициент | Множитель |
| 0, 34 0, 71 0, 63 0, 71 -0, 65 -0, 18 1, 17 -2, 35 0, 75 | 2, 08 0, 17 1, 28 | 1/0, 34 | |
| 1 2, 0881 1, 8529 | 6, 1173 | -0, 71; -1, 17 1/(-2, 1325) | |
| 0 -2, 1325 -1, 4955 0 -4, 7930 -1, 4179 | -4, 1733 -5, 8772 | ||
| 0 1 0, 7013 | 1, 9570 | 4, 7930 1/1, 9434 | |
| 0 0 1, 9434 | 3, 5027 | ||
| 1, 8023 |
Очевидно следующее решение:
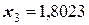 ;
;
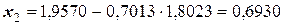 ;
;
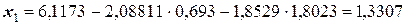 .
.
Мы получили практически тот же результат.
При использовании схемы единственного деления на некотором шаге прямого хода может оказаться, что коэффициент 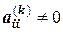 , но существенно меньше по сравнению с остальными элементами матрицы и, в частности, мал по сравнению с элементами первого столбца. Но деление на малую величину может привести к значительным ошибкам округления. Поэтому для их уменьшения и поддержания точности вычислений поступают следующим образом. Среди элементов первого столбца
, но существенно меньше по сравнению с остальными элементами матрицы и, в частности, мал по сравнению с элементами первого столбца. Но деление на малую величину может привести к значительным ошибкам округления. Поэтому для их уменьшения и поддержания точности вычислений поступают следующим образом. Среди элементов первого столбца 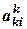 каждой промежуточной матрицы выбирают наибольший по модулю элемент и путем перестановки строк (от этого определитель не меняется) добиваются того, что главный элемент становится ведущим. Такая модификация метода называется методом Гаусса с выбором главного элемента (метод главных элементов).
каждой промежуточной матрицы выбирают наибольший по модулю элемент и путем перестановки строк (от этого определитель не меняется) добиваются того, что главный элемент становится ведущим. Такая модификация метода называется методом Гаусса с выбором главного элемента (метод главных элементов).
Задача 14. Решить систему линейных уравнений методом главных элементов:
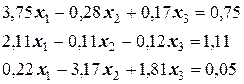 .
.
Решение. Процесс решения представим в виде таблицы 14.
Таблица 14 - Решение задачи 14
| Шаг | Элемент матрицы | Свободный коэффициент | Множитель |
| 3, 75 -0, 28 0, 17 2, 11 -0, 11 -0, 12 0, 22 -3, 17 1, 81 | 0, 75 1, 11 0, 05 | 1/3, 75=0, 2666 | |
| 1 -0, 0747 0, 0453 0 0, 0476 -0, 2156 0 -3, 1536 1, 8000 | 0, 2000 0, 6880 0, 0060 | -2, 11; -0, 22 | |
| 0 -3, 1536 1, 8000 0 0, 0476 -0, 2156 | 0, 0060 0, 6880 | 1/(-3, 1536) | |
| 0 1 -0, 5708 0 -0, 1884 | -0, 0019 0, 6881 | -0, 0476 1/(-0, 1884) | |
| -3, 6523 |
Как видно из таблицы 14, в этом случае появляется дополнительный (второй) шаг, где переставлены местами второе и третье уравнения.
Рассчитываем неизвестные (элементы базовых уравнений в таблице выделены жирным шрифтом):
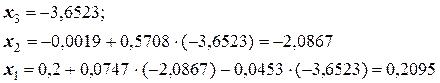
Окончательно получаем:
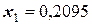 ;
; 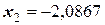 ;
; 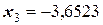 .
.
Проверка: 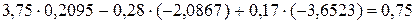
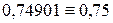 .
.
Полученное решение обеспечивает погрешность по тождествам не выше 0, 02%.
|
|