Регрессионный анализ модели

В результате реализации опытов матрицы планирования получают значения отклика для каждого опыта (строки матрицы плана). На первом этапе определяют дисперсию воспроизводимости, т.е. насколько велико рассеивание результатов экспериментов.

Определение дисперсии воспроизводимости. Каждый эксперимент содержит элемент неопределенности, который оценивается ошибкой эксперимента или ошибкой воспроизводимости. Эта ошибка определяется в результате проведения повторных параллельных опытов, для чего один и тот же опыт воспроизводится в одинаковых условиях несколько раз. По результатам n параллельных опытов определяется среднее арифметическое :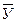

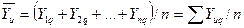(4.72)

где n - количество опытов в одной точке плана,

q - номер строки плана эксперимента,

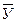- среднее арифметическое значение результата эксперимента,

У_n - экспериментальное значение функции.

Отклонение отдельных значений У_nq от среднего 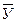_n свидетельствует об изменчивости значений повторных опытов. Для измерения этой изменчивости используют дисперсию (S²) и среднее квадратическое отклонение (S_n):

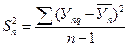(4.73)

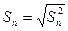(4.74)

Выше изложенное относится к расчету дисперсии в отдельном опыте, т.е. в одной из строк матрицы планирования. Матрица плана состоит из серии опытов, и дисперсия всего эксперимента определяется с учетом дисперсии всех опытов плана, в которых проводились параллельные опыты. Дисперсия эксперимента называется дисперсией отклика S²(У) или дисперсией воспроизводимости (S²_воспр).

Дисперсию воспроизводимости проще всего определить, когда во всех точках плана ставится одинаковое число повторных опытов n. Тогда дисперсия отклика рассчитывается как среднее арифметическое дисперсий отдельных опытов матрицы плана.

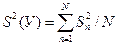(4.75)

где N - число опытов матрицы.

Однако формула справедлива, если все дисперсии 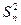однородны, т.е. среди суммируемых дисперсий нет таких, которые бы существенно превышали все остальные. Проверка однородности дисперсий проводится по критерию Кохрена.

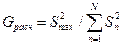(4.76)

где G - расчетное значение критерия Кохрена;

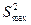- максимальное значение дисперсии;

N - количество точек в плане;

n - количество параллельных опытов в одной точке плана.

Табличное значение критерия Кохрена определяется при заданной доверительной вероятности α (обычно 0, 05) и числе степеней свободы f₁=n-1 и f₂=N. Если расчетное значение критерия меньше табличного, то принимается гипотеза об однородности дисперсий. Если же G_p> G_т, то следует увеличить число параллельных опытов и добиться однородности дисперсий. Если никакими способами нельзя достигнуть воспроизводимости, то математические методы планирования к такому эксперименту применять нельзя.

Если число повторных опытов в различных точках плана неодинаково, то вычислительная процедура усложняется.

В некоторых случаях дисперсия отклика воспроизводимости определяется по n параллельным опытам, поставленным только в одной центральной точке плана и рассчитывается по формуле (4.74).

На втором этапе в соответствии с типом плана вычисляют коэффициенты регрессии и проводят регрессионный анализ полученной модели.

Регрессионный анализ включает в свою очередь три этапа:

- проверку значимости коэффициентов регрессии;

- проверку адекватности уравнения регрессии;

- проверку информационной способности уравнения регрессии.

Проверка значимости проводится для каждого коэффициента с помощью критического значения коэффициента В_{i кр}, ниже которого расчетные значения В_i целесообразно считать равными нулю. Прежде всего, необходимо найти дисперсию коэффициента регрессии 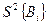. При использовании планов полного факторного эксперимента дисперсии всех коэффициентов равны и вычисляются по формуле:

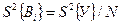(4.77)

и при проведении n параллельных опытов во всех точках плана:

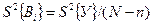(4.78)

Критическое значение коэффициента регрессии вычисляется по формуле:

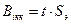(4.79)

где t - табличное значение критерия Стьюдента;

S_э - дисперсия опыта, равная

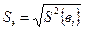(4.80)

Табличное значение критерия Стьюдента определяют при выбранном уровне значимости α (обычно 0, 05) и числе степеней свободы, с которым определяли дисперсию 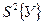(f=N-1, если параллельные опыты не проводились, f=N-(n-1) - при постановке параллельных опытов). Если /В_i/< B_{i кр}, то коэффициент В_i считается незначимым, приравнивается к нулю, исключается из уравнения регрессии.

При использовании планов полиномиальных моделей критические значения коэффициентов определяют по формуле:

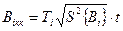(4.81)

где Т_i - диагональные элементы ковариационно-корреляционной матрицы соответствующего плана [30].

Проверка адекватности и информационной ценности выполняется для уравнения, которое содержит только значимые коэффициенты регрессии. Для проверки адекватности модели, иначе говоря, полученного уравнения изучаемому процессу, вычисляется дисперсия неадекватности 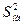. Дисперсия неадекватности характеризует отклонение расчетных значений отклика 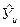от экспериментальных :

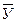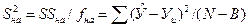(4.82)

где SS_на- сумма квадратов отклонений расчетных значений от средних экспериментальных ;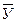

В - число значимых коэффициентов в уравнении регрессии.

Полученное значение 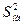сравнивается с дисперсией эксперимента 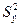, для чего формулируется нуль-гипотеза .

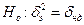Проверка гипотезы проводится по F-критерию (критерию Фишера).

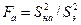(4.83)

Значение F_a сравнивается с F_{табл .}, принятым при f₁=N-B и f₂=f_э, α обычно принимается 0, 05. Если F_a< F_{табл .}, то гипотеза о равенстве дисперсий признается правдоподобной, и, следовательно, предсказываемые уравнением результаты по точности будут не хуже экспериментальных. Уравнение регрессии адекватно описывает результаты эксперимента. Если F_a> F_{табл .}, то гипотеза о равенстве дисперсий отвергается, уравнение считается неадекватным и нуждается в доработке.

Для проверки информационной ценности уравнения формулируется гипотеза о равенстве общей дисперсии и дисперсии неадекватности , которая проверяется по F -критерию:

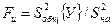(4.84)

Общая по эксперименту дисперсия 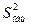рассчитывается по формуле:

(4.85)

где 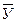- общее среднее по всему эксперименту (плану).

Табличное значение F-критерия принимается при f₁=N-1, f₂=f_на обычно α =0, 05. Если F_и> F_{табл .}, то гипотеза о равенстве дисперсий отвергается, и, следовательно, полученная модель имеет информационную ценность. Если F_и< F_{табл .}, то такая модель не представляет информационной ценности.

Построение графического отклика модели. Для более полного получения информации о полученной модели необходимо построить ее графическое изображение.

В случае однофакторной модели это осуществляется довольно просто. Для этого достаточно менять значения варьируемого фактора (Х) в пределах заданного интервала, подставляя каждый раз в уравнение и вычисляя значения функций (У). Например, интервал изменения Х от -1 до +1, следовательно, подставлять в уравнение можно следующие значения (Х): -1; -0, 5; 0; 0, 5; 1 (подставляют только кодированные значения Х). Затем строят график в координатах Х-У (рисунок 13).

У

Х

-1 -0, 5 0 0, 5 1

Рисунок 13 – Отклик однофакторной модели

Построение графического отклика многофакторной модели значительно сложнее. Графический отклик в этом случае называется изолиниями (если модель двухфакторная) и изображается в квадрате в координатах Х₁-Х₂; или изоповерхностями(если модель трехфакторная) и изображается в кубе в координатах Х₁-Х₂-Х₃.

Если модель многофакторная, то ее необходимо упростить до двух или трехфакторной. Для этого исследователь по-своему усмотрению стабилизирует на определенном уровне те факторы, которые влияют в наименьшей степени. Подставляя в уравнение их кодированные значения, получают выражение с двумя или тремя неизвестными.

Далее определяют значения У, для которых необходимо построить графический отклик. Как правило, для этого из экспериментальных данных определяют минимальное или максимальное значение У. Это будут границы интервала, в котором выбирают любые значения У, для которых будут проводить построение. Принцип выбора значений У изображен на рисунке 14. Интервалы между У₁ У₂ У₃ У₄ У₅ должны быть одинаковыми. Иногда удобно строить графики для нужных марок бетона.

У₁ У₂ У₃ У₄ У₅

У_min У_max

Рисунок 14 – Выбор значений функций для построения графика

Для построения изолиний необходимо, зафиксировав значения функции У ₁, поочередно менять значения фактора Х₁ от -1 до +1, решая уравнение относительно Х₂. Затем меняют Х₂ - решая уравнение относительно Х₁. Таким образом, будет построена изолиния У₁. Далее строят точно также изолинию У₂, затем У₃, и т.д.

Для построения изоповерхностей, прежде всего, фиксируют один из факторов на вертикальной оси. Затем строят изолинии на горизонтальных поверхностях куба. После чего соединяют точки на гранях куба, и получают изоповерхности У₁, У₂, У₃ и т.д. (рисунок 15).

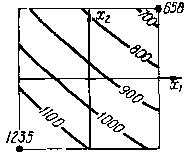
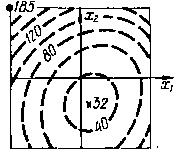
а

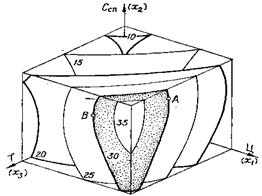
б

Рисунок 15 – Примеры геометрических откликов математических моделей: а - геометрический отклик двухфакторной модели, на плоскости; б - геометрический отклик трёхфакторной модели, в кубе