Принципы имитационного моделирования

Любая модель в принципе имитационная, поскольку она имитирует (подражание) реальный объект. Однако сложились термины “имитационное моделирование” и ”имитационная модель”, которые характерны для вполне определенного класса действий с моделями объектов при решении инженерных, технико-экономических и других задач. Имитация в этом смысле - это анализ системы с помощью вариантных расчетов.

Имитационная модель воспроизводит процесс функционирования объекта во времени, причем имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания во времени, что позволяет по исходным данным получить сведения о состоянии процесса в определенные моменты времени.

Имитационное моделирование является частным случаем цифрового моделирования. Аналитические методы описания и анализа функционирования сложных систем обычно не позволяют учесть особенности организационно-экономических систем, связанные с непрерывностью и дискретностью их элементов, с нелинейностью связи между характеристиками системы, с воздействием многочисленных внешних и внутренних случайных факторов. Для количественного анализа и решения задач строгого аналитического описания, используется имитационное моделирование. Имитационная модель не ставит целью получение точного решения задачи, но она и не связывает себя слишком жесткими математическими предписаниями. Она не решается в аналитическом смысле, а осуществляется именно проигрывание", " прогон" модели. Мощные электронно-вычислительные комплексы дают возможность проводить эксперименты, в которых экспериментатор со своей интуицией и " здравым смыслом" может постоянно контролировать решения изменять исходные предпосылки и логику решения, уточнять требования к выходным данным и т. д.

Имитационное моделирование имеет ряд преимуществ по сравнению с аналитическим: это возможность применять модели, адекватные реальным системам, неограниченно экспериментировать с моделью, внося различные допущения, фактор неопределенности и т.д. (напомним, что аналитическая оптимизация динамических вероятностных процессов наталкивается на очень большие трудности).

В то же время разработка и программирование для ЭВМ имитационных моделей сопряжены обычно с весьма большими затратами труда и времени. Ведь каждая имитационная модель по-своему уникальна, тогда как аналитические модели носят типовой характер, и для их решений на ЭВМ почти всегда можно воспользоваться готовыми прикладными программами, Поэтому, если реальная задача хорошо вписывается в аналитическую модель, то потребность в разработке имитационной модели отпадет. Имитационные модели могут применяться в самых различных областях: для исследования, принятия и проверки решений, полученных другими методами; построения и оценки альтернатив; расчета широкого диапазона прогнозов и оценок будущего состояния производственной системы; оценки долгосрочных последствий от принятого решения; формирования календарного расписания производственной деятельности с вероятностными сроками начала и окончания работ или этапов и т.д. Имитационные модели часто используются в " деловых играх". В этом случае модель, состоящая из большого числа математических уравнений, связывающих причины и следствия, позволяет определить последствия решений, принимаемых участниками игры. Таким образом, имитационный эксперимент - это воспроизведение с помощью ЭВМ модели функционирования некоторой реальной системы.

В технических объектах производится предварительная декомпозиция (de- от слова отмена и т.п.) процесса функционирования объекта на составляющие подпроцессы или подсистемы и для описания тех из них, для которых это возможно и целесообразно, используются функциональные зависимости - аналитические модели (уравнения математической физики, экспериментально-статистические и другие). Для остальных подпроцессов строятся алгоритмы, описывающие правила функционирования подсистем с той или иной степенью формализации.

Имитационная система может рассматриваться как машинный аналог сложного реального процесса. Эксперимент с реальным процессом функционирования системы заменяется машинным экспериментом с математической моделью в режиме имитации этого процесса в ЭВМ.

Имитационное моделирование на ЭВМ является эффективным (а нередко единственным) инструментом исследования и проектирования сложных систем, когда реальный эксперимент невозможен или нецелесообразен по различным причинам. К достоинствам имитационного моделирования, в частности, относится: возможность исследовать поведения объекта в любых условиях (естественно, в области действия модели); значительное сокращение продолжительности испытаний по сравнению с натуральным экспериментом; гибкость структуры модели и возможность замены ее элементов (моделей подсистем, алгоритмов, базы данных и пр.) в ходе экспериментов с целью поиска оптимального варианта, как имитационной модели, так и самой системы при ее проектировании.

К недостаткам имитационного моделирования относится то, что в результате машинной реализации всей цепи анализа системы будет получено частное численное решение, отвечающее фиксированным параметрам системы, уровням факторов, алгоритмам поведения и др. элементам структуры модели. Поэтому для анализа результатов процесса функционирования системы необходимо проводить имитационный эксперимент многократно, варьируя исходные условия каждой реализации. Это требует значительных затрат машинного времени на проведение имитационных экспериментов.

Одна из наиболее развитых областей применения имитационных моделей при решении инженерных задач - это исследование процессов функционирования систем, подверженных случайным воздействиям, методом статистического моделирования. При этом исходные условия каждой реализации задаются как случайные величины, закон распределения которых известен, а результаты множества таких реализаций, как выборочная совокупность числовых значений выхода системы. Для этой совокупности нужно найти статистические оценки неизвестного распределения (по тем же алгоритмам, которые применяются для обработки результатов натурного эксперимента) и сделать инженерные выводы о поведении системы.

Проведение имитационного эксперимента слагается из следующих этапов.

1 Описание явления или процесса, подлежащего моделированию.

2 Определение количественных характеристик, доступных наблюдению или измерению.

3 Проведение необходимых упрощений, выбор типа модели (т.е. создание собственно математической модели).

4 Перевод модели на язык ЭВМ - выбор языка программирования и создание программы.

5 Анализ результатов расчета. Сравнение с результатами натурного эксперимента или косвенными данными, имеющимися в распоряжении исследователя.

Модели принято подразделять на детерминированные и вероятностные.

Пример. Простейшим примером детерминированной модели может служить модель системы, описываемой дифференциальным уравнением или системой таких уравнений. Так, малые колебания маятника (точка массой m находится на конце стержня длиной l, другой конец которого закреплен так, что маятник в целом может отклоняться на угол θ) описываются дифференциальным уравнением

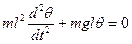(4.93)

где t - время,

g -ускорение силы тяжести.

Примером такого же типа является широко известное описание распространения тепла в стержне с помощью уравнения теплопроводности

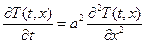(4.94)

где Т - температура,

х - координата точки стержня,

a - константа, определяемая свойствами материала.

Детерминированные модели описанного выше типа исследуются аналитически, если они достаточно просты, и с использованием ЭВМ, если вместо одного уравнения в описании модели фигурируют, например, системы большого числа уравнений и искомые функции зависят от большого числа переменных. Имитационный эксперимент с помощью ЭВМ состоит для таких моделей в численном решении соответствующих уравнений. При этом, как правило, требуется замена исходной системы уравнений разностной системой или другая дискретизация, что вносит дополнительную погрешность, обусловленную не существом задачи, а выбором численного метода.

Примерами вероятностных моделей могут служить, в первую очередь, системы массового обслуживания (СМО). Такие системы часто невозможно исследовать другими способами, кроме имитационного моделирования. Простейшие СМО характеризуются:

а) случайным потоком заявок. Заявки поступают в случайные моменты времени (которые образуют скачкообразный процесс);

б) случайным временем обслуживания. Каждая заявка либо застает обслуживающее устройство свободным и немедленно начинает обслуживаться, либо становится в очередь. Либо время обслуживания, либо интервалы между поступлениями заявок могут быть детерминированы, но, когда детерминированы и время, и интервалы, задача не представляет интереса.

ЭВМ снабжены датчиками случайных чисел. С помощью известных приемов, описанных в руководствах по статистическому моделированию, по одной или некоторому множеству реализаций равномерно распределенной случайной величины могут быть получены реализации случайной величины или случайного вектора с заданными законами распределения.

Все это позволяет строить имитационную модель случайного процесса, протекающего в СМО, наблюдая изменения ее состояний во времени.

Пример - имитационная модель размещения туристов в гостинице. При проектировании современных туристических комплексов важно заранее предвидеть узкие места в обслуживании. С этой целью предварительно моделируют процесс обслуживания. При моделировании размещения туристов в реальной или проектируемой гостинице необходимо задать:

· закон, по которому прибывают туристы, и интервалы времени между прибытием отдельных туристов или групп. Обычно такой закон задают, исходя из статистической обработки реальных потоков туристов. Он зависит от вида транспорта и расписания прибытия поездов, самолетов и т. п.;

· распределение вероятностей категорий туристов (иностранные туристы, правительственные делегации, крупные группы и т. п.);

· количество свободных мест в гостинице в начальный момент времени;

· время оформления туриста, которое зависит от категории туриста и ряда других факторов.

Модель может быть более или менее подробной. Обычно в ЭВМ хранятся сведения о туристах, размещенных и находящихся в процессе размещения в определенные моменты времени (например, каждые 20 мин.). Каждую количественную характеристику модели можно рассматривать как случайный процесс и применять для обработки данных методы, разработанные в статистике случайных процессов. Моделирование, подобное описанному, применяется для решения вопросов о числе мест в проектируемой гостинице, числе лифтов, размере холла, численности персонала и т. п.

Существенно менее разработанной является теория планирования имитационного эксперимента. Имитационный эксперимент предоставляет больше возможностей для планирования, чем натурный, так как при имитационном эксперименте распределения случайных величин находятся в распоряжении экспериментатора, а при натурном даются природой.

Отсюда следует, прежде всего, что все методы планирования эксперимента, разработанные для натурного эксперимента, могут быть использованы и в имитационном эксперименте.

Известные методы планирования подразделяются на общие методы и методы, специфические для марковских моделей [13].

Как и в общем случае, непосредственной целью планирования имитационного эксперимента является минимизация затрат. Если результатом экспериментирования является одно число - оценка математического ожидания моделируемой случайной величины ξ по N ее независимым реализациям, то затраты на проведение имитационного эксперимента (трудоемкость) определяются величиной tDξ, где t - среднее время ЭВМ, необходимое для получения одной реализации ξ.

Далее рассматриваются наиболее простые и распространенные методы планирования имитационных экспериментов.

Метод зависимых испытаний. Пусть модель зависит от некоторого числового параметра х, а в результате моделирования на ЭВМ мы получаем реализацию случайного процесса ξ (x, ω), где ω = ω (α ₁, …, α _N1); через α ₁, α ₂, … здесь и далее обозначены псевдослучайные числа, получаемые последовательно с помощью программного датчика. При изучении зависимости модели от параметра х планирование состоит в том, что моделирование при разных значениях X производится по одной и той же последовательности случайных чисел.

Так, вычисления ξ (x₀, ω) и ξ (x₀+h, ω) по одной итой же последовательности случайных чисел ω дают возможность оценить разность E[ξ (x₀+h, ω) - ξ (x₀+ω)] с большей точностью, чем при вычислении ξ (x₀+h, ω) и ξ (x₀, ω ') где ω и ω ' независимы. Это необходимо иметь в виду при проведении имитационных экспериментов с целью оптимизации.

Метод противоположной переменной. Как правило, целью моделирования является оценка некоторых средних характеристик модели. Отображение ω = ω (α ₁, …, α _N1) сводит (по крайней мере, теоретически) задачу к задаче оценивания интеграла по единичному гиперкубу. Размерность гиперкуба заранее неизвестна. Тем не менее, можно применять квадратурные формулы со случайными узлами, которые нечувствительны к размерности интеграла.

Так, например, наряду с реализацией случайного процесса ξ (α ₁, …, α _N1) можно использовать ξ (1 - α ₁, 1 - α ₂, 1 - α _N). Процесс ½ [ ξ ((α ₁, …, α _N) + ξ (1 - α ₁, …, 1 - α _N)] будет иметь те же средние характеристики, но с меньшими дисперсиями. Известны более сложные квадратурные формулы, применяемые для аналогичных целей.

Расщепление и рулетка. Этот общий прием уместно пояснить на простейшем примере системы массового обслуживания с одним прибором. Пусть в систему через случайные промежутки времени поступают заявки, которые ставятся в очередь, если имеются заявки, уже находящиеся в очереди или в процессе обслуживания. Если очереди нет и прибор свободен, то заявка немедленно поступает на обслуживание. Состояние системы обычно характеризуют числом п заявок, находящихся в системе в данный момент. Моделирование состоит в прослеживании изменений числа п. Интерес представляют вероятности p_n(t) того, что в системе в момент времени t находится п требований. Если для системы существует стационарный режим, то существует предел р_п= 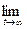p_n(t). Если заявки поступают редко и обслуживаются быстро, то р_п при большом п - величина малая, и оценить ее трудно (большого числа заявок в системе практически не бывает).

В этих случаях можно поступать так. Разделим время функционирования системы на отрезки длины Т и зададимся некоторыми п = N и т. Если k ₀ —первое значение такое, что по истечении времени k₀T число требований в системе превзойдет N, то с этого момента времени будем рассматривать т идентичных систем, снабжая все характеристики «весом» по 1 /т каждую. Некоторый момент времени k₁T окажется опять таким, что число требований, хотя бы в одной из систем, будет 2 N (k₁ > k). Эту систему мы опять делим на т (или какое-нибудь другое число т₁) систем, домножая ее характеристики на 1/т. Этот прием и носит название «расщепление». При этом выделяются перспективные для нас системы.

Очевидно, что при таком расщеплении накапливается с течением времени много систем, для нас неперспективных. Среди них проводится «лотерея». «Выигравшая» система сохраняется, и ей приписывается вес, равный суммарному весу всех участвовавших в лотерее систем. Это и есть «рулетка».

Методика выбора параметров расщепления и рулетки и составляет задачу планирования эксперимента, которая изучена недостаточно.

Перечисленные методы применимы при моделировании широкого класса систем. Во всяком случае, все агрегативные системы могут моделироваться с их использованием.

В основе статистического моделирования лежит универсальный численный метод решения математических задач при моделировании случайных величин - метод Монте-Карло.

Метод Монте-Карло дал интересные и полезные инженерные результаты при использовании в режиме имитации моделей заполнения объема материала зернами разных размеров и форм, при моделировании деформации и прочности бетона методами механики разрушения, при исследовании проницаемости бетона, при анализе однородности смешивания технологических смесей и в ряде других материаловедческих и технологических задач.

При анализе «n» результатов натурального эксперимента в одной точке k -факторного пространства предполагается, что все эти k исследуемых рецептурно-технологических факторов имеют неизменные уровни и именно эта стабильность определяет центр их группирования - среднее значение выхода системы 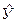. В то же время рассеяние результатов в некотором интервале {Y_V(min) Y_v(max)} обуславливается неконтролируемым действием случайных факторов 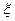; оно оценивается среднеквадратическим отклонением S{ 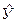}, которое приравнивается к ошибке эксперимента S_э.

Новое среднее значение выхода системы 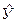при переходе ее в другую точку факторного пространства, как известно, достаточно просто предсказывается по экспериментально-статистической модели. Можно оценить ошибку предсказания S{Ŷ }, связанную с постоянной в данной области ошибкой эксперимента S_э и с мерой точности модели d, зависящей от свойств плана эксперимента и от координат точки предсказания.

Однако, ни ошибка эксперимента S_э, ни ошибка предсказания S{Ŷ } не могут охарактеризовать устойчивость выхода системы Y к неизбежным колебаниям во времени тех k факторов X_i, которые и в натурном эксперименте, и при прогнозе Y по модели принимались фиксированными (X_i=const (i = 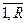)). Эти колебания факторов во времени X_i(τ _ε ) приведут к дополнительному рассеянию значений Y; при этом рецептурно-технологическое решение (X_i=const) следует считать неустойчивым, если малым колебаниям X_i(τ _ε ) будет соответствовать большое рассеяние Y_ε , оцениваемое среднеквадратичным отклонением S{Y_ε }, коэффициентом вариации υ {Y_ε } и т.п. При сравнении двух рецептурно-технологических решений А и В, обеспечивающих равные средние значения выхода Y^(A)=Y^{(Β )} , предпочтительнее то, которое имеет большую устойчивость (меньшее S{Y_ε } и т.п.).

Решение проблемы устойчивости при натурном эксперименте с системой весьма трудоемко и требует специального планирования эксперимента, основанного на многомерном дисперсионном анализе. Поэтому разработана ориентированная на машинный эксперимент методика, согласно которой:

на первом этапе строится экспериментально-статистическая k-факторная модель поведения системы;

на втором этапе независимо анализируются закономерности распределения случайных значений уровней факторов X_iε , характерных для данного производства;

на третьем этапе генерируются в ЭВМ случайные числа для имитации в соответствии с результатами второго этапа случайных колебаний факторов X_iε вокруг выбранного рецептурно-технологического решения (X_i=const);

на четвертом этапе методом Монте-Карло по модели «проигрываются» n реализаций, соответствующих случайным уровням k факторов, т.е. n раз производится расчет ;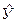

на пятом этапе по алгоритмам, применяемым при статистическом анализе результатов натурного эксперимента в одной точке, оцениваются статистические характеристики генерированной в ходе реализации метода Монте-Карло выборочной совокупности 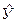и рассчитывается критерий устойчивости рецептурно-технологического решения.

При имитационном моделировании вообще, а при реализации метода Монте-Карло на экспериментально-статистических моделях в частности, целесообразно применять все идеи и методы математической теории эксперимента, что позволяет резко уменьшить число вариантов, а в ряде задач получить простые полиномиальные описания сложных вероятностных ситуаций. При планировании имитационного эксперимента в качестве переменных могут выступать не только рецептурно-технологические факторы, изменяющие координаты точек Х_i, но и характеристики диапазонов варьирования случайных величин p_i, а также сами законы распределения f(P_i) этих величин.

Опыт решения задач анализа устойчивости рецептурно-технологических решений методом Монте-Карло показывает эффективность и полезность такого подхода, однако его методическое и программное обеспечение пока далеки от совершенства.

Метод Монте-Карло широко применяют при моделировании структуры и свойств композиционных материалов. Реальные искусственные строительные материалы неоднородны по структуре. Так, бетоны на уровне макроструктуры состоят из зерен крупного заполнителя (щебня) разного размера и формы и цементно-песчаной матрицы. Характерный дефект структуры – трещины на границе раздела матрицы и заполнителя, в частности, из-за седиментационных явлений при твердении бетона. На следующем уровне (называемом мезоструктурой) легко обнаруживается, что цементно-песчаная матрица неоднородна – она состоит из зерен крупнодисперсионного наполнителя (песка) и матрицы из цементного камня, в которой распределены некоторые дефекты в виде трещин и крупных пор.

На уровне микроструктуры сама по себе цементная матрица также неоднородна – она состоит из затвердевшего цементного геля с твердыми включениями в виде зерен цементного клинкера и тонкомолотого наполнителя. Характерные элементы структуры на этом уровне – поры различной конфигурации и технологические трещины. В зависимости от цели исследования в структуре реальных материалов могут быть выявлены как иные уровни, так и иные структурные элементы.

Проблема моделирования структуры и ее влияния на свойства материала является одной из самых актуальных в материаловедении, однако она пока находится в начальной стадии разрешения. Целесообразно выделить несколько базовых задач в этой проблеме. Во-первых, в структуре должны быть выявлены характерные элементы, которым придается идеализированная геометрическая форма (сфероиды, цилиндры и т.п.) с заданным законом распределения размеров и которые наделяются комплексом свойств (плотностью, модулем упругости, проводимостью и т.п.) с уровнями, распределенными по известным законам. Во-вторых, структурные элементы должны быть «расставлены» в пространстве (ограниченная плоскость, куб, сфера, изделие сложной конфигурации и т.п.) по некоторым правилам, в число которых входит

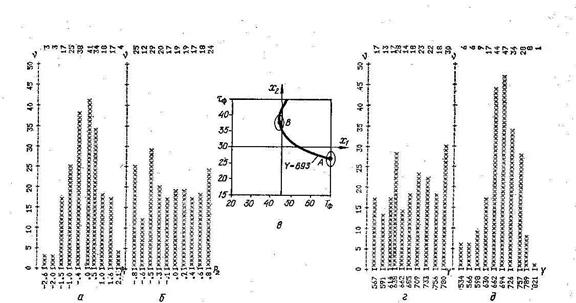Рисунок 20 – Анализ устойчивости технологических решений (точки А и В) с помощью метода Монте-Карло: а – гистограмма генерированных случайных величин для имитации колебаний Т_ф; б – то же для τ _ф; в – положение сравниваемых решений А и В на изолинии Y=693; г – гистограмма результирующих колебаний Y в точке А; д – то же, в точке В.

случайное расположение i - го элемента в незанятой другими элементами области. В-третьих, должны быть установлены закономерности взаимодействия элементов структуры (как между собой, так и со средой, внешней по отношению к материалу) при изменении напряжений и деформаций, при тепломассообмене и пр. В-четвертых, необходимо составить алгоритмы пошагового изменения структурных элементов и характеров взаимосвязей между ними при пошаговом изменении внешней среды. Все эти задачи, особенно третьей и четвертой групп, очень сложны и пока, вообще говоря, еще не сформулированы достаточно полно и конкретно.

Некоторые представления, связанные с моделированием структуры, поясняются на рисунке 21.

В плоский контейнер размером А*А (без потери общности А=1), у которого левая стенка и дно совпадают с осями координат, в случайном порядке «упаковываются» элементы структуры.

Для круглого зерна 1 (пора, наполнитель и т.п.) задаются три случайных числа, которые определяют случайный выбор одного из возможных радиусов R⁽¹⁾, расстояние центра зерна от левой стенки 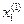и от дна 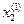. Поскольку контейнер пока пустой, то все эти числа запоминаются. Следующее зерно 2 считается неупакованным и не запоминается, поскольку оно пересеклось со стенкой (нарушено условие 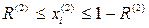). Зерно 3 укладывается в контейнер, так как оно попало на пустое место (выполнено условие 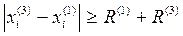), а вот информация о зерне 4 не запоминается, так как оно пересекает уже уложенное зерно 1. Повторяя процедуру n раз, можно «заполнить» контейнер, промоделировав случайную укладку зерен, радиусы которых подчиняются заданному закону распределения, и тем самым оценить, в частности, пустотность (пористость, проницаемость и т.п.) материала. Следует отметить, что существуют алгоритмы, «сдвигающие» зерно, попавшее на занятое место, до тех пор, пока оно не упакуется. Кроме того, у каждого зерна 1, 2, 3, … может быть свой случайно распределенный или связанный с размером зерна уровень физического свойства (модуль упругости, электропроводность, плотность), что расширяет круг решаемых с помощью такого «контейнера» инженерных задач.

Структурные элементы могут иметь форму, отличную от сферической. Для фиксации прямоугольника 5 (кристалл, волокно и т.п.) кроме координат центра x_i нужно задать еще три случайные величины: размер одной из сторон l, соотношение между сторонами l: b, угол наклона j к оси координат. Для фиксации многоугольника 6 (крупный заполнитель и т.п.) дополнительно задаются радиус описанной окружности R⁽⁶⁾ и n координат (четыре угла j _i) его вершин.

Важнейшими структурными элементами, особенно в задачах моделирования деформации и прочности материалов методом механики разрушения, являются дефекты – трещины в матрицах разного структурного уровня. Трещины на контактах матрицы и включения (зерно 7 на рисунке 21, а) распределяются в случайном порядке сначала по зернам, а потом на одну из граней выбранного зерна.

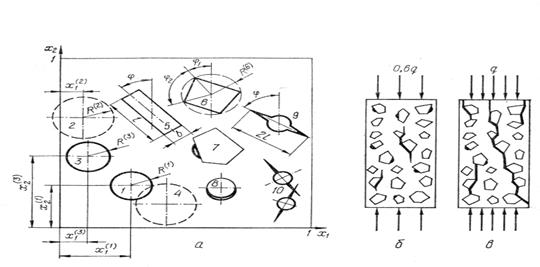
Рисунок 21 - Имитация структуры материала: а – упаковка контейнера элементами структуры; б, в – изменения в структуре при изменении внешней нагрузки

Если имитируются трещины, возникающие от седиментационного расслоения смеси, то они располагаются всегда на нижней части зерна (8 на рисунке 21, а). Трещины около отверстий (пор) моделируются структурным элементом 9, для которого обычно задается случайный угол наклона j, а также, при необходимости, случайные радиусы пор R и длина трещины l. Допустимо такое расположение двух пор, при котором трещины пересекаются (элемент 10 на рисунке 21, а), образуя непрерывную слившуюся трещину.

В зависимости от постановки задач моделирования структуры и свойств композиционных материалов могут быть распределены и другие элементы: ленты разной длины и конфигурации, каналы с узлами запирания, сети и т.п., а сам контейнер может быть объемным.

Алгоритм, описывающий закономерности поведения структуры при изменении условий внешней среды, строится, как правило, прежде всего, как пошаговый процесс поведения каждого типа элементов структуры (с учетом возможного взаимодействия с контактирующими соседними элементами). Поскольку единичный элемент достаточно сильно упрощен, то для описания происходящих с ним изменений построить математическую модель не так сложно, как для структуры в целом. При этом можно использовать любые модели, но наиболее удачными, как правило, являются модели концептуальные, в которых четко прослеживаются физические особенности процесса. Например, пора 1 в нагруженном материале описывается формулами технической механики как круговой концентратор напряжений. После того, как пиковые напряжения превысят некоторый уровень, и появится радиальная трещина, произойдет переход к другим формулам технической механики, описывающим деформации элемента 9. Когда длина трещины значительно превысит радиус отверстия или две соседние трещины сольются в элемент 10, то для описания процесса деформации потребуется третий комплекс формул (таблиц, графиков и т.п.).

После того, как произошедшие со всеми индивидуальными элементами изменения зафиксированы в машине, они могут быть тем или иным образом интегрированы (или усреднены, или представлены мажорантами и т.п.) и переданы для обсуждения оператору-исследователю. Если после данного шага никаких существенных перемен (границы которых заранее определены исследователем) не произошло, то будет автоматически совершен следующий шаг в изменении условий внешней среды и так последовательно (рисунке 21, б, в) до наступления критического состояния в структуре (разрушение, электрический пробой, сквозной проход жидкости и др.). Уровень влияния внешней среды (нагрузка, электрическое напряжение, давление жидкости и др.), при котором достигается критическое состояние, а также общий характер процесса поведения материала при воздействии внешней среды сравниваются с результатами натурного эксперимента. На основе такого сравнения и принимается решение об адекватности модели.

Преимущества вышеизложенного принципиально нового подхода к анализу структуры и свойств композиционных материалов очевидны. Необходимо подчеркнуть две особенности такого моделирования: во-первых, на любом этапе исследования в связи с появлением более сильных физических гипотез или точных формул можно некоторую часть имитационной модели заменить; во-вторых, в ходе реализаций статических испытаний можно выявить те сочетания структуры элементов и влияния внешней среды, при которых моделируемое явление идет по неизвестному направлению, что открывает возможности целенаправленного создания новых материалов и технологий [7].