
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Билет 21.
|
|
1) Область D на плоскости Oxy - простой (правильной) в направлении оси Oy, если любая прямая, проходящая через внутреннюю точку области D и параллельная оси Oy, пересекает границу D в двух точках
Простая (правильная) область в направлении оси Ox: любая прямая, проходящая через внутреннюю точку области D и параллельная оси Oх, пересекает границу D в двух точках.
Теорема о переходе от двойного интеграла к повторному. Пусть D - простая в направлении оси Oy и Ox области. Тогда двойной интеграл от непрерывной функции по области D равна повторному интегралу от той же функции по области D: 
2)Гармонические поля. Скалярное поле  называется гармоническим, если оно удовлетворяет уравнению Лапласа
называется гармоническим, если оно удовлетворяет уравнению Лапласа  , или
, или  . Векторное поле
. Векторное поле  (M) называется гармоническим, если оно является градиентом некоторой гармонической функции, т.е.
(M) называется гармоническим, если оно является градиентом некоторой гармонической функции, т.е.  (M)
(M) 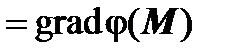 , где
, где  .
.
Гармоническое векторное поле одновременно потенциально и соленоидально, так как 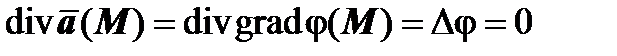 . Верно и обратное: если
. Верно и обратное: если  (M) одновременно и потенциально, и соленоидально, то оно является гармоническим. Из потенциальности
(M) одновременно и потенциально, и соленоидально, то оно является гармоническим. Из потенциальности  , из соленоидальности
, из соленоидальности 
 , т.е.
, т.е.  - гармонический потенциал. Каждая координата гармонического векторного поля является гармонической функцией.
- гармонический потенциал. Каждая координата гармонического векторного поля является гармонической функцией.
3) Теорема. Для того, чтобы бесконечно дифференцируемая функция 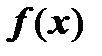 в окрестности точки
в окрестности точки  разлагалась в ряд Тейлора, необходимо и достаточно, чтобы
разлагалась в ряд Тейлора, необходимо и достаточно, чтобы  .
.
Доказательство. Необходимость. Пусть в окрестности точки  функция
функция 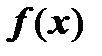 представлена в виде сходящегося к этой функции ряда Тейлора
представлена в виде сходящегося к этой функции ряда Тейлора 
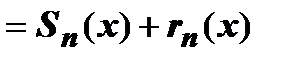 , где
, где  - частичная сумма ряда,
- частичная сумма ряда,  - его остаток. Так как
- его остаток. Так как 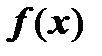 имеет требуемое количество производных, она может быть представлена и в виде формулы Тейлора с остаточным членом в форме Лагранжа:
имеет требуемое количество производных, она может быть представлена и в виде формулы Тейлора с остаточным членом в форме Лагранжа:  . Сравнивая эти представления, получаем
. Сравнивая эти представления, получаем 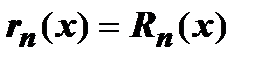 . Из сходимости ряда к
. Из сходимости ряда к 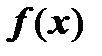 следует, что
следует, что  , что и требовалось доказать.
, что и требовалось доказать.
Достаточность. Если  , то
, то  , т.е. остаток ряда стремится к нулю при
, т.е. остаток ряда стремится к нулю при  , т.е. ряд сходится к функции
, т.е. ряд сходится к функции 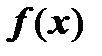 .
.
4)  эллиптический парабалоид
эллиптический парабалоид
5)  ds=
ds= 

6)  возьмём ряд из модулей, где аn=
возьмём ряд из модулей, где аn= 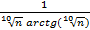
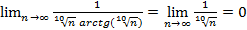 арктангенс стремится к π /2, сходится по признаку Лейбница.
арктангенс стремится к π /2, сходится по признаку Лейбница.
 возьмём ряд из модулей, где аn=
возьмём ряд из модулей, где аn= 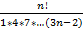 по признаку Даламбера:
по признаку Даламбера:

Расходится.
Билет 22
|
|