Степенные ряды.

Определение. Степенным рядом называется функциональный ряд вида ,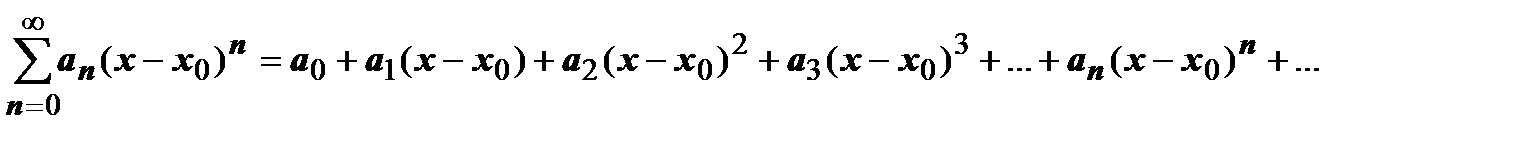

где 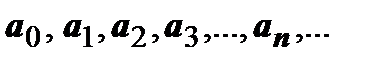- постоянные (коэффициенты ряда), 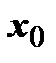- фиксированное число (центр сходимости). Степенной ряд имеет по меньшей мере одну точку сходимости - точку .

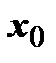Радиус сходимости, интервал сходимости и область сходимости степенного ряда. Из теоремы Абеля следует, что существует такое число R (возможно, ) такое, что при степенной ряд сходится, при ряд расходится. Действительно, пусть в точке ряд сходится, в точке ряд расходится. Рассмотрим точку , расположенную между областями, в которых установлена сходимость и расходимость. В точке числовой ряд 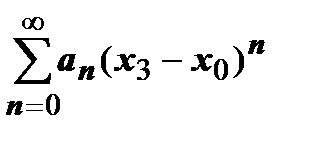либо сходится, либо расходится. Если он сходится, то мы можем перенести точку в точку ; если ряд в точке расходится, мы переносим в точку . Продолжая этот процесс, мы сблизим точки и , эта граница и определит число R.

Определение. Число R такое, что при степенной ряд сходится, при ряд расходится, называется радиусом сходимости. Интервал называется интервалом сходимости степенного ряда.

Сходимость ряда в концевых точках интервала сходимости должна исследоваться отдельно. В зависимости от поведения ряда на концах интервала сходимости область сходимости степенного ряда может быть одной из следующих: , , , .

Итак, для определения области сходимости степенного ряда надо найти его интервал сходимости R, затем исследовать поведения ряда в концевых точках интервала сходимости .

Примеры. 1. . Для определения радиуса сходимости этого ряда целесообразно применить признак сходимости Дирихле. Однако этот признак, как и многие другие, может применяться только к положительному ряду, поэтому выпишем ряд, состоящий из абсолютных величин членов исследуемого ряда: . Применяем признак Дирихле: . Следовательно, . Мы нашли радиус сходимости R =3 и интервал сходимости . Исследуем поведение ряда на концах интервала: , ряд сходится. , ряд сходится абсолютно. Область сходимости - интервал [-7, 7].

3)