
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача №10. Основание пирамиды - равнобедренный прямоугольный треугольник
|
|
Основание пирамиды - равнобедренный прямоугольный треугольник. Все боковые рёбра пирамиды равны 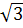 . Найдите наибольший возможный объём такой пирамиды.
. Найдите наибольший возможный объём такой пирамиды.
Решение:
Примем высоту DO данной пирамиды за x, где 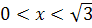 . Из прямоугольного треугольника ADO находим AO2=3-x2, а из равнобедренного треугольника ACO находим AC2=2AO2 =2(3-x2). Таким образом, требуется найти наибольшее значение функции V(x)=
. Из прямоугольного треугольника ADO находим AO2=3-x2, а из равнобедренного треугольника ACO находим AC2=2AO2 =2(3-x2). Таким образом, требуется найти наибольшее значение функции V(x)= 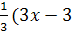 на интервале (0;
на интервале (0; 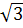 ).
). 
ar w: top=" 1134" w: right=" 850" w: bottom=" 1134" w: left=" 1701" w: header=" 720" w: footer=" 720" w: gutter=" 0" /> < w: cols w: space=" 720" /> < /w: sectPr> < /w: body> < /w: wordDocument> "> 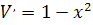 ;
;  ;
;
На интервале (0; 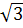 ) функция V(x) непрерывна, имеет единственный экстремум в точке x = 1 и этот экстремум - максимум.
) функция V(x) непрерывна, имеет единственный экстремум в точке x = 1 и этот экстремум - максимум.
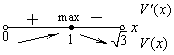
Следовательно, V(1)=  - наибольшее значение данной функции на интервале (0;
- наибольшее значение данной функции на интервале (0; 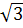 ).
).
Ответ: 
Замечание: Рассмотренный выше алгоритм нахождения наибольшего (наименьшего) значения функции на интервале применим и для нахождения наибольшего (наименьшего) значения функции на отрезке, если функция непрерывна на этом отрезке и имеет на нём единственный экстремум.
|
|