Теоретические сведения. Важной экономической проблемой является своевременное обновление оборудования

Важной экономической проблемой является своевременное обновление оборудования. Старение оборудования включает физический и моральный износ, в результате чего растут затраты на ремонт и обслуживание, снижаются производительность труда и ликвидная стоимость. Задача заключается в определении оптимальных сроков замены старого оборудования.

Критерием оптимальности являются доход от эксплуатации оборудования (задача максимизации) либо суммарные затраты на эксплуатацию в течение планируемого периода (задача минимизации).

Предположим, что планируется эксплуатация оборудования в течение некоторого периода времени продолжительностью п лет. Оборудование имеет тенденцию с течением времени стареть и приносить все меньший доход r(t), где t — возраст оборудования.

При этом есть возможность в начале любого года продать устаревшее оборудование за цену S(t), которая также зависит от возраста, и купить новое оборудование за цену Р. Под возрастом оборудования понимается период эксплуатации оборудования после последней замены, определенный в годах.

Требуется найти оптимальный план замены оборудования на новое так, чтобы суммарный доход за все п лет был бы максимальным, учитывая, что к началу эксплуатации возраст оборудования составлял t₀ лет.

Исходными данными в задаче являются:

r(t) - доходот эксплуатации в течение одного года оборудования;

t - возраст оборудования;

S(t) - остаточная стоимость оборудования;

Р - цена нового оборудования;

t₀ - начальный возраст оборудования.

При составлении динамической модели выбора оптимальной стратегии обновления оборудования процесс замены рассматривается как многошаговый и период эксплуатации разбивается на п шагов.

Процесс оптимизации проводим с последнего шага k = n.

Переменная t в данной задаче является переменной состояния системы на k -омшаге.

Переменной управления на k -омшаге является логическая переменная, которая может принимать одно из двух значений: сохранить (С) или заменить (3) оборудование в начале k -ого года.

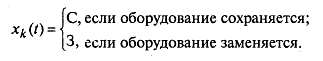
Функцию Беллмана F_k(t) определяют как максимально возможный доход от эксплуатации оборудования за годы с k -ого по n -й, если к началу k -ого возраст оборудования составлял t лет. Применяя то или иное управление, система переходит в новое состояние.

Так, например, если в начале k -ого года оборудование сохраняется, то к началу (k+1)-го года его возраст увеличится на единицу (состояние системы станет t+1), в случае замены старого оборудования новое достигнет к началу (k+1)-го года возраста t₁ = 1 год.

На этой основе можно записать уравнение, которое позволяет рекуррентно вычислить функцию Беллмана, опираясь на результаты предыдущего шага. Для каждого варианта управления доход определяется как сумма двух слагаемых — непосредственного результата управления и его последствий.

Если в начале каждого года сохраняется оборудование, возраст которого t лет, то доход за этот год составит r(t). К началу(k+1) - го года возраст оборудования достигнет (t+1) и максимально возможный доход за оставшиеся годы (с (k+1) -го по n -й) составит F_k+1(t+1).

Если в начале k -го года принято решение о замене оборудования, то продается старое оборудование возраста t лет по цене S(t), приобретается новое за Р единиц, а эксплуатация в течение k -го года нового оборудования принесет прибыль г (0). К началу следующего года возраст оборудования составит 1 год, и за все оставшиеся годы с (k+1) -го по n -й максимально возможный доход будет F_k+1(1).

Из двух возможных вариантов управления выбирается тот, который приносит максимальный доход. Таким образом, функциональное уравнение Беллмана на каждом шаге управления можно записать так:

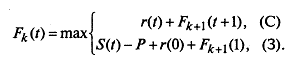
Функция F_k(t) ) вычисляется на каждом шаге управления для всех 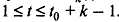. Управление, при котором достигается максимум дохода, является оптимальным.

Для первого шага условной оптимизации при k=n функция представляет собой доход за последний n -й год:

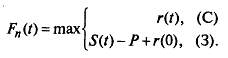
Значения F_k+1(…..)=0, так как периода свыше n не существует.

Максимум дохода достигается при некотором управлении, применяя которое на первом году, мы определяем возраст оборудования к началу второго года. Для этого возраста оборудования выбирается управление, при котором достигается максимум дохода за годы со второго по n -й и т д. В результате чего на этапе безусловной оптимизации определяются те годы, в начале которых следует произвести замену оборудования.