
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нерівність трикутника
|
|
Добре відомо, що для трьох довільних точок 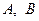 та
та 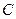 виконується нерівність
виконується нерівність 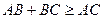 (нерівність буде строгою, якщо точка
(нерівність буде строгою, якщо точка 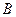 не лежать між двома іншими точками). Звідси отримуємо, що довжина ламаної не більша за відстань між її кінцями. Ці елементарні міркування часто є ключовими при доведенні нерівностей для відстаней.
не лежать між двома іншими точками). Звідси отримуємо, що довжина ламаної не більша за відстань між її кінцями. Ці елементарні міркування часто є ключовими при доведенні нерівностей для відстаней.
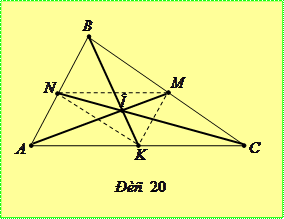 Задача 5.1.1. Довести, що довжини медіан
Задача 5.1.1. Довести, що довжини медіан 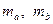 і
і 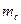 та його периметр
та його периметр 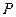 задовольняють нерівності
задовольняють нерівності
 .
.
Доведення. Нехай у трикутнику 
 ;
; 
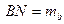 ,
, 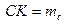 - медіани (рис. 20). Із
- медіани (рис. 20). Із 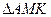 маємо
маємо
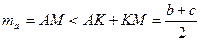 .
.
Аналогічно отримуємо нерівності 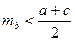 та
та 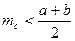 . Додаючи одержані співвідношення, отримуємо праву частину нерівності, що доводиться. Із
. Додаючи одержані співвідношення, отримуємо праву частину нерівності, що доводиться. Із  маємо
маємо
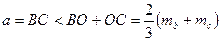 .
.
Таким же чином дістаємо нерівності 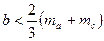 ,
, 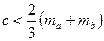 , додаючи які та попередню, отримуємо ліву частину співвідношення, що доводиться.
, додаючи які та попередню, отримуємо ліву частину співвідношення, що доводиться.
Згадуючи співвідношення, які виражають довжини медіан через сторони трикутника, зокрема 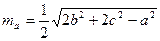 , на основі доведеного твердження можна говорити, що нами реалізовано геометричне доведення алгебраїчної нерівності
, на основі доведеного твердження можна говорити, що нами реалізовано геометричне доведення алгебраїчної нерівності
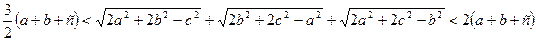 ,
,
де числа 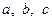 додатні і такі, що сума двох із них більша від третього.
додатні і такі, що сума двох із них більша від третього.
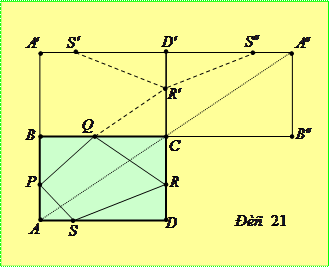
Задача 5.1.2. У прямокутнику 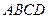 на сторонах
на сторонах 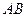 ,
,  ,
, 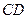 та
та 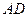 вибрано точки
вибрано точки 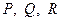 та
та 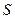 (по одній на кожній стороні). Довести, що периметр одержаного чотирикутника не менший
(по одній на кожній стороні). Довести, що периметр одержаного чотирикутника не менший 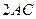 .
.
Доведення. Симетризуємо прямокутник 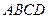 відносно сторони
відносно сторони  , а потім – відносно прямої
, а потім – відносно прямої 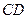 . При цьому утворяться нові прямокутники
. При цьому утворяться нові прямокутники 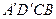 та
та 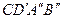 (рис. 21). Очевидно, що периметр чотирикутника
(рис. 21). Очевидно, що периметр чотирикутника 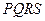 буде дорівнювати
буде дорівнювати
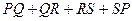 =
= 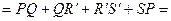

і оскільки 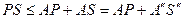 , то він не буде перевищувати довжини ламаної
, то він не буде перевищувати довжини ламаної 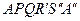 , яка в свою чергу не перевищує довжини відрізка
, яка в свою чергу не перевищує довжини відрізка 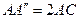 .
.
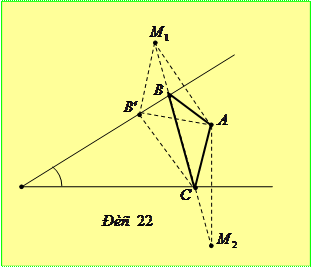
Задача 5.1.3. Дано гострий кут і точку 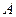 всередині нього. Знайти на сторонах кута такі точки
всередині нього. Знайти на сторонах кута такі точки  та
та 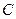 , щоб периметр трикутника
, щоб периметр трикутника  був мінімальним.
був мінімальним.
Розв’язання. Нехай задана точка 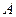 всередині кута
всередині кута 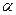 . Симетризуючи її відносно сторін кута, отримаємо точки
. Симетризуючи її відносно сторін кута, отримаємо точки 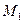 та
та 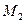 . Проведемо пряму
. Проведемо пряму 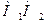 , яка перетне сторони кута у деяких точках
, яка перетне сторони кута у деяких точках 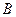 та
та 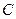 (рис. 22). Покажемо, що трикутник
(рис. 22). Покажемо, що трикутник  - шуканий.
- шуканий.
Насамперед, зауваживши, що симетричні відносно прямої відрізки рівні, отримуємо 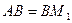 та
та 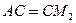 . Тому периметр
. Тому периметр
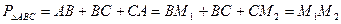 .
.
Для іншого положення точки  на стороні кута (наприклад, для точки
на стороні кута (наприклад, для точки 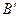 ) дістаємо
) дістаємо
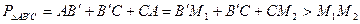 .
.
Аналогічно збільшується периметр трикутника  при зміні положення точки
при зміні положення точки 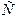 на другій стороні кута. Таким чином, точки
на другій стороні кута. Таким чином, точки 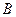 та
та  - шукані.
- шукані.
Очевидно, що якщо заданий кут гострий, то пряма  завжди перетне сторони кута, тому поставлена задача матиме єдиний розв’язок.
завжди перетне сторони кута, тому поставлена задача матиме єдиний розв’язок.
|
|